Не увидела связи между прямоугольником 
и рассматриваемым. потому решение может не очень красивое.
Заметим, что есть узловая точка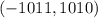 
, которая делит прямоугольник на два (по диагонали), в которых количества пересекаемых квадратиков равны и потому можно посчитать только в одном из них.
Рассмотрим две горизонтальные прямые и диагональ. Внутри они образуют прямоугольный треугольник, один из катетов которого (горизонтальный) равен 
. Ну а тогда второй равен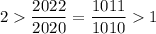 
, а потому количество пересекаемых квадратов в каждой из горизонталей либо 
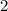, либо 
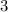. Поймем, когда их три.
Три квадратика образуются тогда и только тогда, когда точки пересечения соседних вертикалей находятся между соседними горизонталями. Для этого требуется, чтобы точка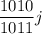 
(
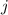-- номер вертикали) достаточно далеко находилась от ближайшего целого, то есть дробная часть 
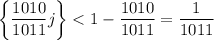, что равносильно тому, что 
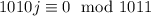, поскольку иначе число 
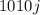дает остаток, не меньший . Но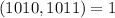 
, а потому единственными решениями будут 
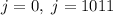, то есть крайние вертикали, что не подходит. Значит, во всех горизонталях задеваются ровно два квадрата, а значит всего 
.
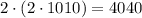1)
64 = 2 * 2 * 2 * 2 * 2* 2
54 = 2 * 3 * 3 * 3
НСК ( 64; 54) = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3 = 1728
2)
100 = 2 * 2 * 5 * 5
125 = 5 * 5 * 5
НСК( 100; 125) = 5 * 5 * 5 * 2 * 2 = 500
3)
95 = 5 * 19
114 = 2 * 3 * 19
НСК ( 95; 114 ) = 2 * 3 * 19 * 5 = 570
4)
121 = 11 * 11
88 = 2 * 2 * 2 * 11
НСК ( 121; 88 ) = 11 * 11* 2 * 2* 2 = 968
5)
168 = 2 * 2 * 2 * 3 * 7
140 = 2 * 2 * 5 * 7
НСК (168; 140 ) = 2 * 2 * 2 * 3 * 7 * 5 = 840
6)
144 = 2 * 2 * 2 * 2 * 3 * 3
324 = 2 * 2 * 3 * 3 * 3 * 3
НСК ( 144; 324 ) = 2 * 2 * 3 * 3 * 3 * 3 *2 *2 = 1296
7)
125 = 5 * 5 * 5
225 = 3 * 3 * 5 * 5
НСК ( 125; 225 ) = 3 * 3 * 5 * 5 * 5 = 1125
8)
185 = 5 * 37
111 = 3 * 37
НСК ( 185; 111 ) = 5 * 37 * 3 = 555
