Решить .в магазине было 68 ящиков красных яблок и 30 ящиков зеленых.продали 40 ящиков.сколько ящиков яблок осталось

👇

Увидеть ответ

Ответ:

concon1233

04.08.2021

1) 68+30=98-ящиков всего
2)98-40=58-ящиков осталось

4,4(87 оценок)

Ответ:

МамкаДраконов

04.08.2021

1) 68+30=98 (всего)
2) 98-40=58
ответ: 58 ящиков

4,6(25 оценок)

Открыть все ответы

Ответ:

1705081705

04.08.2021

1) 270 | 2 324 | 2 540 | 2

135 | 3 162 | 2 270 | 2

45 | 3 81 | 3 135 | 3

15 | 3 27 | 3 45 | 3

5 | 5 9 | 3 15 | 3

1 3 | 3 5 | 5

270 = 2 · 3³ · 5 1 1

324 = 2² · 3⁴ 540 = 2² · 3³ · 5

НОК (270, 324, 540) = 2² · 3⁴ · 5 = 1620 - наименьшее общее кратное

1620 : 270 = 6 1620 : 324 = 5 1620 : 540 = 3

- - - - - - - - - - - - - - -

150 | 2 375 | 3 600 | 2

75 | 3 125 | 5 300 | 2

25 | 5 25 | 5 150 | 2

5 | 5 5 | 5 75 | 3

1 1 25 | 5

150 = 2 · 3 · 5² 375 = 3 · 5³ 5 | 5

600 = 2³ · 3 · 5²

НОД (150, 375, 600) = 3 · 5² = 75 - наибольший общий делитель

150 : 75 = 2 375 : 75 = 5 600 : 75 = 8

2) 420 | 2 252 | 2

210 | 2 126 | 2

105 | 3 63 | 3

35 | 5 21 | 3

7 | 7 7 | 7

1 1

420 = 2² · 3 · 5 · 7 252 = 2² · 3² · 7

НОД (420, 252) = 2² · 3 · 7 = 84 - наибольший общий делитель

420 : 84 = 5 252 : 84 = 3

- - - - - - - - - - - - - - -

НОК (420, 252) = 2² · 3² · 5 · 7 = 1260 - наименьшее общее кратное

1260 : 420 = 3 1260 : 252 = 5

3) 40 | 2 56 | 2

20 | 2 28 | 2

10 | 2 14 | 2

5 | 5 7 | 7

1 1

40 = 2³ · 5 56 = 2³ · 7

НОД (40, 56) = 2³ = 8 - наибольший общий делитель

40 : 8 = 5 56 : 8 = 7

- - - - - - - - - - - - - - -

НОК (40, 56) = 2³ · 5 · 7 = 280 - наименьшее общее кратное

280 : 40 = 7 280 : 56 = 5

4,6(92 оценок)

Ответ:

Ivankozyr69gmail

04.08.2021

Матрица, соответствующая данной квадратичной форме:
$A=\begin{pmatrix}
 1 & -1 & 3 & -2 \\
 -1 & 1 & -2 & 3 \\
 3 & -2 & 1 & -1 \\
 -2 & 3 & -1 & 1 
\end{pmatrix}$

Нужно найти собственные числа и собственные вектора этой матрицы. Собственные числа находим из уравнения det(A - λE) = 0:
$\det (A-\lambda E)=\begin{vmatrix}1-\lambda & -1 & 3 & -2 \\ -1 & 1-\lambda & -2 & 3 \\ 3 & -2 & 1-\lambda & -1 \\ -2 & 3 & -1 & 1-\lambda\end{vmatrix}=\dots$

Прибавим к первой строке все остальные строки, после вынесения общего множителя обнулим первый столбик во всех строках, кроме первой:
$\dots=\begin{vmatrix}1-\lambda & 1-\lambda & 1-\lambda & 1-\lambda \\ -1 & 1-\lambda & -2 & 3 \\ 3 & -2 & 1-\lambda & -1 \\ -2 & 3 & -1 & 1-\lambda\end{vmatrix}=\\=(1-\lambda)\begin{vmatrix}1 & 1 & 1 & 1 \\ -1 & 1-\lambda & -2 & 3 \\ 3 & -2 & 1-\lambda & -1 \\ -2 & 3 & -1 & 1-\lambda\end{vmatrix}=\\=(1-\lambda)\begin{vmatrix}1 & 1 & 1 & 1 \\ 0 & 2-\lambda & -1 & 4 \\ 0 & -5 & -2-\lambda & -4 \\ 0 & 5 & 1 & 3-\lambda\end{vmatrix}=\dots$

Раскладываем определитель по первому столбцу. Опустим пока множитель (1 - λ), сложим прибавим к третьей строчке вторую, вынесем общий множитель и обнулим третий столбец везде, кроме последней строки:
$\dfrac{\dots}{(1-\lambda)}=\begin{vmatrix}2-\lambda & -1 & 4 \\ -5 & -2-\lambda & -4 \\ 5 & 1 & 3-\lambda\end{vmatrix}=\begin{vmatrix}2-\lambda & -1 & 4 \\ -5 & -2-\lambda & -4 \\ 0 & -1-\lambda & -1-\lambda\end{vmatrix}=\\=(-1-\lambda)\begin{vmatrix}2-\lambda & -1 & 4 \\ -5 & -2-\lambda & -4 \\ 0 & 1 & 1\end{vmatrix}=(-1-\lambda)\begin{vmatrix}2-\lambda & -5 & 0 \\ -5 & 2-\lambda & 0 \\ 0 & 1 & 1\end{vmatrix}=\dots$

Раскладываем определитель по третьему столбцу, после отбрасывания множителей остается определитель матрицы 2x2, который равен
$(2-\lambda)^2-(-5)^2=(-3-\lambda)(7-\lambda)$

Итак,
$\det (A-\lambda E)=(1-\lambda)(-1-\lambda)(-3-\lambda)(7-\lambda)=0\\
\lambda_{1,2,3,4}\in\{\pm 1,-3,7\}$

Находим собственные векторы:
1) с.ч. = 1
Сумма всех строк равна 0, выкинем последнюю. Приведем матрицу к красивому виду (насколько сможем):
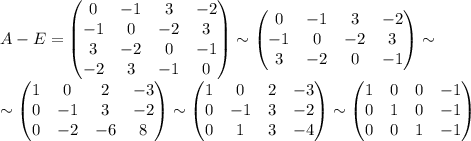
$A-E=\begin{pmatrix} 0 & -1 & 3 & -2 \\ -1 & 0 & -2 & 3 \\ 3 & -2 & 0 & -1 \\ -2 & 3 & -1 & 0 \end{pmatrix}\sim \begin{pmatrix} 0 & -1 & 3 & -2 \\ -1 & 0 & -2 & 3 \\ 3 & -2 & 0 & -1 \end{pmatrix}\sim \\\sim \begin{pmatrix} 1 & 0 & 2 & -3 \\ 0 & -1 & 3 & -2 \\ 0 & -2 & -6 & 8 \end{pmatrix} \sim \begin{pmatrix} 1 & 0 & 2 & -3 \\ 0 & -1 & 3 & -2 \\ 0 & 1 & 3 & -4 \end{pmatrix} \sim \begin{pmatrix} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{pmatrix}$

Из полученного вида матрицы получаем, что уравнению удовлетворяют все вектора вида (a, a, a, a); с.в. (1, 1, 1, 1)

2) c.ч. = -1
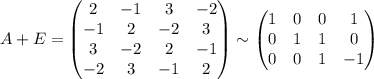
$A+E=\begin{pmatrix} 2 & -1 & 3 & -2 \\ -1 & 2 & -2 & 3 \\ 3 & -2 & 2 & -1 \\ -2 & 3 & -1 & 2 \end{pmatrix}\sim \begin{pmatrix} 1&0&0&1\\0 & 1 & 1 & 0 \\ 0 & 0 & 1 & -1 \end{pmatrix}$
с.в. (1, 1, -1, -1)

3) с.ч. = -3
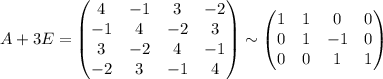
$A+3E=\begin{pmatrix} 4 & -1 & 3 & -2 \\ -1 & 4 & -2 & 3 \\ 3 & -2 & 4 & -1 \\ -2 & 3 & -1 & 4 \end{pmatrix}\sim \begin{pmatrix} 1&1&0&0\\0 & 1 & -1 & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix}$
с.в. (1, -1, -1, 1)

4) с.ч. = 7
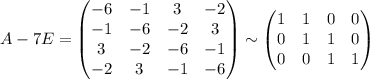
$A-7E=\begin{pmatrix} -6 & -1 & 3 & -2 \\ -1 & -6 & -2 & 3 \\ 3 & -2 & -6 & -1 \\ -2 & 3 & -1 & -6 \end{pmatrix}\sim \begin{pmatrix} 1&1&0&0\\0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix}$
c.в. (1, -1, 1, -1)

Собственные вектора уже ортогональны, но еще не отнормированы. Длина каждого равна 1/2, так что окончательно получаем, что под действием замены
$\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}=\begin{pmatrix}\frac12&\frac12&\frac12&\frac12\\\frac12&\frac12&-\frac12&-\frac12\\\frac12&-\frac12&-\frac12&\frac12\\\frac12&-\frac12&\frac12&-\frac12\end{pmatrix}\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}$
(по столбцам записаны собственные векторы) квадратичная форма примет вид
y_1^2-y_2^2-3y_3^2+7y_4^2