ответ:
. дан отрезок ав. с циркуля и линейки разделите его на три равные части.
построение. 1) проведем отрезок ав;
2) из точки а проведем окружность произвольного радиуса, которая пересекает отрезок ав в точке д, а его продолжение за точку а - в точке с;
3) из точек с и д проводим окружности радиусом большим сд, пересекающиеся в точках м и n, через полученные точки проводим прямую мn, которая перпендикулярна прямой ав;
4) возьмем произвольную точку р прямой мn и проведем через нее прямую рк, перпендикулярную прямой мn; прямые ав и рк будут параллельны;
5) от начала р луча рм отложим три равных отрезка рр1, р1р2, р2р3, каждый из которых меньше отрезка ав;
6) через точки р3 и в проведем прямую, которая пересечет прямую мn в точке q;
7) проводим прямые р2q и р1q, которые и разделят отрезок ав на три равные части, аа1 = а1а2 = а2в. нетрудно доказать, используя подобие треугольников, что построенные части отрезка ав действительно равны.
пошаговое объяснение:
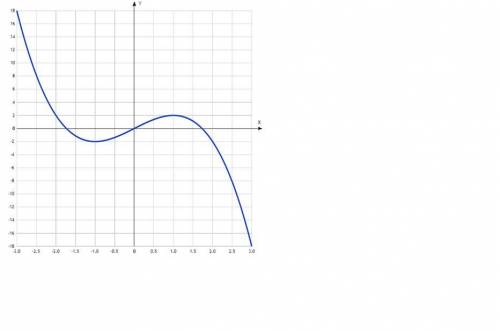
Точка пересечения графика функции с осью координат Оу:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в -x3+3x.
у =-0^3+3*0 = 0,
Результат: y=0. Точка: (0; 0).
Точки пересечения графика функции с осью координат Ох:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
-x^3 + 3x= 0
Решаем это уравнение и его корни будут точками пересечения с осью Ох:
-x(x^2 – 3) = 0.
Получаем 3 точки: х = 0, х = √3 и х = -√3.
Результат: y=0. Точки: (0; 0), (√3; 0) и (-√3; 0).
Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y' = -3x^2 + 3 = 0
Решаем это уравнение и его корни будут экстремумами:
-3(х^2-1) = 0,
х1 = 1, х2 = -1.
Результат: точки: (1; 2) и (-1; -2).
Интервалы возрастания и убывания функции:
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
На промежутках находим знаки производной
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -2 -1 0 1 2
y' = -9 0 3 0 -9
• Минимум функции в точке: х = -1,
• Максимум функции в точке: х = 1.
• Возрастает на промежутке: (-1; 1).
• Убывает на промежутках: (-∞; -1) U (1; +∞).
Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции.
Нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:
y'' = -6x = 0.
Решаем это уравнение и его корни будут точками, где у графика перегибы:
x=0. Точка: (0; 0).
Интервалы выпуклости, вогнутости:
Найдем интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках изгибов.
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
• Вогнутая на промежутках: (-∞; 0),
• Выпуклая на промежутках: (0; ∞).
Вертикальные асимптоты – нет.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+oo и x->-oo. Соответствующие пределы находим:
• lim -x3+3x, x->+∞ =- ∞, значит, горизонтальной асимптоты справа не существует
• lim -x3+3x, x->-∞ = ∞, значит, горизонтальной асимптоты слева не существует.
Наклонные асимптоты графика функции.
Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы:
• lim -x3+3x/x, x->+∞ = -∞, значит, наклонной асимптоты справа не существует
• lim -x3+3x/x, x->-∞ = ∞, значит, наклонной асимптоты слева не существует
Четность и нечетность функции:
Проверим функцию - четна или нечетна с соотношений f(-x)=f(x) и f(-x)=-f(x). Итак, проверяем:
• f(-x) = -(-x)3+3(-x) = x3-3x - нет f(-x) ≠ f(x).
• f(-x) = -(-x)3+3(-x)) = -(-x3+3x) – да f(-x)=-f(x), значит, функция является нечётной.
Все законы проходят чтения, обсуждаются и изменяются и принимаются в гос думе и совете федераций, в затем утверждаются президентом.
Важно знать, что если закон не противоречит конституции, то президент не имеет права не подписывать этот закон.
Парламент собственно этим и занят - обсуждает законодательные инициативы. Президент у нас по большей части занят внешней политикой: решает международные проблемы, выстраивает отношения, встречается с главами других стран. Кроме президента в повестку задач внешней политики включены Министерство иностранных дел, министерство обороны, главы ФСБ и МВД.
Внутренней политикой у нас в основном занимается парламент и правительство под руководством премьера (председатель правительства).
Разные сферы жизни разделены на ведомства - министерства. Главы министерств - министры, составляют кабинет министров. Там есть и министр промышленности, министр сельского хозяйства, министр связи, здравоохранения, культуры и другие. Есть также ещё ряд заместителей председателя, которые чем-то занимаются.
Огромный аппарат ведомств.
Самый интересный министр - это министр по делам открытого правительства. Чем он занимается не знает даже сам министр по делам открытого правительства и весь кабинет министров.