ответ:ответ=15см квадрат.
Пошаговое объяснение:
сначала мы дорисовываем так что бы получился прямоугольник первая чать. Как только мы дорисовали мы найдем площадь прямоугольника
S=2"3=6см в квадрате потом делим на 2 получится 3 см в квадрате,
потом просто находим S прямоугольник.
третья часть поступаем как с первой дорисовываем часть до прямоугольника находим S потом делим на два получилось 12см квадрате. Потом дели на два получилось 6см квадрате
найдем S фигуры:
3+6+6=15 см квадрате.
ответ: S= 15 см в квадрате
1. в) -5:2<0
-2.5<0
2. a) -8*9=-72
б) -8,35*100 = -(8,35*100) = -835
в) -36:4 = -9
г) -60,4 : (-0,4) = 60,4 : 0,4 = 151
3. а) 10х=-5
х= -  = -
= -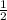
б) х:(-0,2) = 8
х:(-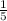 ) = 8
) = 8
-х*5 = 8
-5х = 8
х = -
4. а) -6,2*3 = -18,6
б) -19,68 : (-0,8) = 19,68 : 0,8 = 24,6
в) 16,32: (-16) = -(16,32: 16) = -1,02
5. а) 0,5*(-36)*2 = -(0,5*36*2)= -(18*2) = -36
б) -500*37,38(-2)*0,1 = 18690*2*0,1=1869*2=2
6. (0,8-2,86:2,6)*(3,04-7,02) = (0,8-1,43)(-3,98) = -0,63*(-3,98) = 2,5
7. |-3x-1.5| = 0.5
-3x-1.5 = 0.5 -3x-1.5 = -0.5
-3x= 0.5 + 1.5 -3x = -0.5 + 1.5
-3x = 2 -3x = 1
x= - 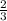 x = -
x = -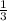
Проведем прямую через точку C параллельно DG; пусть она пересекает отрезок AD в точке F. Применим теорему о пропорциональных отрезках к углу BAG, стороны которого пересекают параллельные прямые DG и FC:
DF:FA=GC:CA; DF:FA=4:1. То есть точка F делит отрезок DA на отрезки, один из которых в 4 раза длиннее другого. Чтобы найти их длины, делим DA на 5 частей, DF забирает себе 4 из них, оставляя одну часть отрезку FA. Итак, DF=4/5.
Применим теорему о пропорциональных отрезках к углу ABC, стороны которого пересекают параллельные прямые DE и FC:
BE:EC=BD:DF; BE:EC=4:(4/5)=5:1. То есть точка E делит BC в отношении 5:1. Иными словами, BE - это 5/6 от BC.
Итак, BD=(4/5)BA; BE=(5/6)BC;
Переходим к нахождению площадей:
ответ: 0,6