SABCD -правильная четырехугольная пирамида. Постройте сечение пирамиды плоскостью, проходящей через DO (точка О-внутренняя точка отрезка SC) и перпендикулярной плоскости ABC.Если искомая площадь перпендикулярна плоскости АВС, то она перпендикулярна плоскости АВСD. Проведем диагональное сечение АSС пирамиды .О лежит на ребре SC и принадлежит этому диагональному сечению. Опустим в плоскости ∆ ASC из О перпендикуляр ОН на АС (он лежит в плоскости диагонального сечения, перпендикулярной основанию, параллелен высоте пирамиды, и потому перпендикулярен её основанию). Через D и Н проведем прямую до пересечения с ВС в точке К. Соединим D, О и К. Через 3 точки можно провести плоскость, притом только одну. Плоскость ∆ DОК - сечение пирамиды. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.Плоскость ∆ DОК проходит через ОН, перпендикулярный плоскости основания, и является искомым сечением
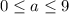
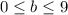
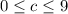
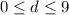
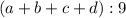или 
∈ 
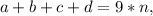
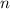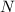
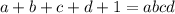
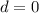, то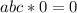 
- такого быть не может, значит этот случай нам не подходит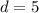
, 
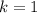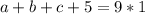, тогда 
⇒ 
⇒ 
, 
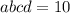
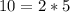
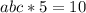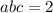
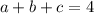
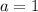
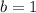
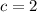
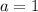
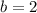
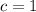
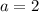
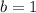
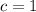
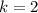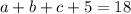, тогда 
⇒ 
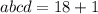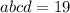
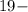простое число, произведение можно представить только в виде простых множителей
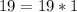так как a, b, c, d - цифры, тогда этот случай не подходит 
, 
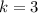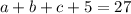, тогда 
⇒ 
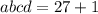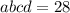
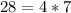, но один из множитель должен быть 5 - этот случай не подходит 
, 
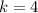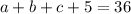, тогда 
⇒ 
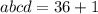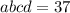
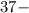простое число, произведение можно представить только в виде простых множителей
так как a, b, c, d - цифры, тогда этот случай не подходит 
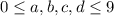и 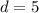последний случай можно было не рассматривать как и все оставшиеся.
(195+a)*3=195*3+3а=585+3а
a=96
585+3*96=873
a=128
585+128*3=969
a=115
585+115*3=930
2)Найди значения выражения при наименьшем значении a.
а=96 наименьшее число 873
При каком значении a результатом будет наибольшее трёхзначное число?
а=128 наибольшее 969
3) Выбери своё значения a. Найди значение выражения для этого числа
а=105
(195+105)*3=300*3=900