Имеется 8 карточек. на них записываются по одному каждое из чисел 1, -2, -3, 5, -6, 7, -8, 9. карточки переворачивают и перемешивают. на их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 5, -6, 7, -8, 9. после этого числа на каждой карточке складываются, а полученные восемь сумм перемножаются. а) может ли в результате получиться 0? б) может ли в результате получиться 1? в) какое наименьшее целое неотрицательное число может в результате получиться?

👇

Ответ:

ValeriaAstahova99

21.10.2020

A) Произведение равно 0 если хотя бы один из множителей равен 0. Каждый из восьми множителей есть сумма двух чисел. Сумма же равна нулю лишь в том случае, когда складываются противоположные числа
х+(-х)=0
Но в нашей последовательности нет ни одной пары взаимопротивоположных чисел. Значит, 0 в результате не может быть никогда.

б) Поскольку наши числа целые, то их сумма будет также целым числом. А произведение целых чисел будет равно 1 лишь в том случае, когда они все по модулю равны 1. А это условие не выполняется. Например, если на одной стороне написано -3, то, какое бы число не было написано на противоположной стороне, модуль суммы будет отличаться от 1. Следовательно, 1 в результате получиться не может

в) произведение будет минимальным, когда величина множителей минимальна. Попробуем составить минимальное произведение. Начнем с большего числа. Если на одной стороне 9, то на другой -8, для -8 на другой стороне или 9, или 7. Но если возьмем 7, то 9 будет в паре с таким числом, которое даст сумму больше 1. Поэтому выбираем 9. Ну и дальше по аналогии:
1 сторона: 9 -8 7 -6 5 -3 -2 1
2 сторона: -8 9 -6 7 -3 5 1 -2
сумма 1 1 1 1 2 2 -1 -1
Произведение будет равно 4. Это произведение будет минимальным.

4,5(60 оценок)

Открыть все ответы

Ответ:

schooll13

21.10.2020

Пояснение:

Сравнение чисел.

• Положительные числа.

При сравнении положительных чисел больше то, у которого больше модуль (само число). Положительные числа всегда больше "0" (нуля).

• Отрицательные числа.

При сравнении отрицательных чисел больше то, у которого меньше модуль (само число). Отрицательные числа всегда меньше "0" (нуля).

• Положительные числа всегда больше отрицательных.

Модуль - расстояние на координатной прямой от нуля до некой точки.

Модуль всегда равняется положительному числу, (НЕ МОЖЕТ РАВНЯТЬСЯ ОТРИЦАТЕЛЬНОМУ ЧИСЛУ! т.к. по сути это расстояние), т.е. модуль положительного числа равен положительному числу, а модуль отрицательного числа тоже равен положительному числу.

Например, |12| = 12; |- 64| = 64; и т.д.

Решение / ответ:

• 15 ✓ - 33,12;

15 > - 33,12.

• - 15 ✓ - 19;

- 15 > - 19.

• - 33 ✓ 0;

- 33 < 0.

• - 5,5 ✓ 5,05;

- 5,5 < 5,05.

• 1,001 ✓ 0;

1,001 > 0.

• - 18,02 ✓ - 18,03;

- 18,02 > - 18,03.

• 333 ✓ 555;

333 < 555.

Удачи Вам! :)

4,5(15 оценок)

Ответ:

obuhovasveta

21.10.2020

$\beta\in[0;1]:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{n}}=\alpha$

Тогда, по признаку Коши, при 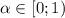$\alpha\in[0;1)$ ряд сходится, при 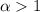$\alpha 1$ расходится.

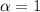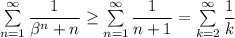При $\alpha=1$ имеем $\sum\limits_{n=1}^\infty\dfrac{1}{\beta^n+n}\geq \sum\limits_{n=1}^\infty\dfrac{1}{n+1}= \sum\limits_{k=2}^\infty\dfrac{1}{k}$ Гармонический ряд расходится, а тогда исходный ряд расходится по признаку сравнения.

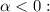
$\alpha$

При 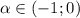$\alpha\in(-1;0)$ ряд сходится, т.к. ряд из модулей (по доказанному выше) сходится.

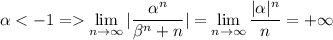$\alpha\lim\limits_{n\to\infty}{|\dfrac{\alpha^n}{\beta^n+n}|}=\lim\limits_{n\to\infty}{\dfrac{|\alpha|^n}{n}}=+\infty$ необходимое условие не выполнено, а значит ряд расходится.

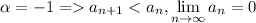$\alpha=-1= a_{n+1}$ , а тогда по признаку Лейбница ряд сходится.

$\beta1:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n}}=\dfrac{\alpha}{\beta}$

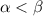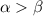Тогда при $\alpha$ ряд сходится, при $\alpha\beta$ расходится.

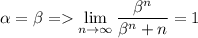$\alpha=\beta=\lim\limits_{n\to\infty}{\dfrac{\beta^n}{\beta^n+n}}=1$ - необходимое условие не выполнено, ряд расходится.

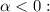
$\alpha$

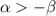Тогда при $\alpha-\beta$ ряд сходится.

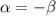При $\alpha=-\beta$ необходимое условие не выполнено, ряд расходится.

$\alpha|\alpha|=-\alpha\beta\\=\lim\limits_{n\to\infty}{|\dfrac{\alpha^n}{\beta^n+n}|}=\lim\limits_{n\to\infty}{\dfrac{|\alpha|^n}{\beta^n}}=+\infty$ необходимое условие не выполнено, ряд расходится.