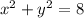Путешестренник проехал 40 км. это 20 % всего пути путешественника . сколько километров состовляет весь путт ?

👇

Увидеть ответ

Ответ:

СанькаДьяченко

12.03.2020

40 км—20%
Х км—100%

40*100:20=200 км

4,4(28 оценок)

Открыть все ответы

Ответ:

Marketing23

12.03.2020

$x^{2} + y^{2} = 8$ — уравнение окружности с центром 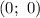$(0; \ 0)$ и радиусом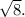 $\sqrt{8}.$

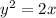$y^{2} = 2x$ — уравнение параболы

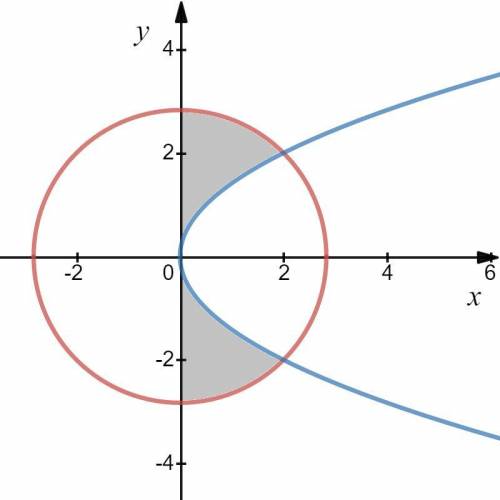
Изобразим графики данных уравнений и найдем площадь образовавшейся фигуры в правой полуплоскости.

Выразим ординаты данных уравнений:

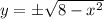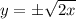
$y = \pm\sqrt{8 - x^{2}}$ и $y = \pm\sqrt{2x}$

Так как имеем симметричные фигуры, найдем площадь 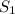$S_{1}$ одной из них. Общая их площадь 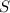будет состоять из площади двух 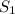$S_{1}$ , то есть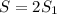 $S = 2S_{1}$

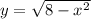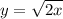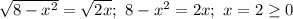
Тогда $y =\sqrt{8 - x^{2}}$ и $y = \sqrt{2x}$ . Поэтому $\sqrt{8 - x^{2}} = \sqrt{2x}; \ 8 - x^{2} = 2x; \ x = 2 \geq 0$

Так как окружность вытесняет больше площади, чем парабола, то имеем разность их площадей, определяющаяся через определенный интеграл:

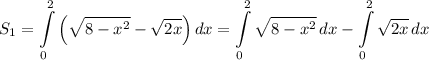
$S_{1} = \displaystyle \int\limits^{2}_{0} {\left(\sqrt{8 - x^{2}} - \sqrt{2x} \right)} \, dx = \int\limits^{2}_{0} {\sqrt{8 - x^{2}}} \, dx - \int\limits^{2}_{0} { \sqrt{2x} } \, dx$

Найдем первый интеграл геометрически: площадь круга находится по формуле 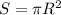$S = \pi R^{2}$ , где 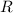— радиус круга. Тогда четверть круга: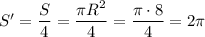 $S' = \dfrac{S}{4} = \dfrac{\pi R^{2}}{4} = \dfrac{\pi \cdot 8}{4} = 2\pi$

Найдем второй интеграл по формуле Ньютона-Лейбница:

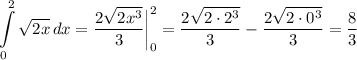
$\displaystyle \int\limits^{2}_{0} { \sqrt{2x} } \, dx = \dfrac{2\sqrt{2x^{3}}}{3} \bigg|_{0}^{2} = \dfrac{2\sqrt{2 \cdot 2^{3}}}{3} - \dfrac{2\sqrt{2 \cdot 0^{3}}}{3} = \dfrac{8}{3}$

Таким образом, 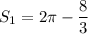$S_{1} = 2\pi - \dfrac{8}{3}$ кв. ед.

Тогда 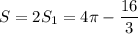$S = 2S_{1} = 4\pi - \dfrac{16}{3}$ кв. ед.

ответ: 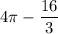$4\pi - \dfrac{16}{3}$ кв. ед.

Найти площадь фигуры, лежащей в правой полуплоскости и ограниченной окружностью x^2+y^2=8 и параболо

4,8(43 оценок)

Ответ:

roker62

12.03.2020

×19
46
+114
  76
  874
9 Умножаем на 6, получаем 54, 4 пишем, а 5 запоминаем.
6 умножаем на 1, получаем 6 да еще 5, равно 11
4 умножаем на 9, получаем 36, 6 пишем, а 3 запоминаем.
4 умножаем на 1, получаем 4 да еще 3, равно 7.
Сложение:
4 сносим в ответ.
6+1=7
7+1=8
ответ: 874

35
* 27
+245
  70
945
7 умножаем на 5, получаем 35, 5 пишем, а 3 запоминаем.
7 умножаем на 3, получаем 21 да еще 3, равно 24
2 умножаем на 5, получаем 10, 0 пишем, 1 запоминаем.
2 умножаем на 3, получаем 6 да еще 1, равно 7
Сложение:
5 сносим в ответ.
4+0=4
2+7=9
ответ: 945

42
*23
+126
84
966
3 умножаем на 2, получаем 6.
3 умножаем на 4, получаем 12.
2 умножаем на 2, получаем 4.
2 умножаем на 4, получаем 8.
Сложение:
6 сносим в ответ.
2+4=6
1+8=9
ответ: 966

  25
   *25
  125
+50
625
5 умножаем на 5, получаем 25, 5 пишем, а 2 запоминаем.
5 умножаем на 2, получаем 10 да еще 2, равно 12.
2 умножаем на 5, получаем 10, 0 пишем, а 1 запоминаем.
2 умножаем на 2, получаем 4 да еще 1, равно 5.
Сложение:
5 сносим в ответ.
2+0=2
1+5=6
ответ: 625

4,4(39 оценок)

Это интересно:

Компьютеры-и-электроника

16.05.2022

Как использовать команду установки воспроизведения атрибутов файлов для обнаружения вирусов?...

Семейная-жизнь

11.06.2020

Как прекратить воевать со своим братом или сестрой...

Хобби-и-рукоделие

06.06.2021

Как поместить яйцо в бутылку: советы и хитрости...

Финансы-и-бизнес