Question

Найти высоту конуса наименьшего объема,описанного около полушара радиуса r (цент основания конуса лежит в центре основания шара)

Answer 1

Дан полушар  с радиусом  R = OC    и   описанный около  него конус  с радиусом  основания  r = OA   и высотой  h = OM.

Построим сечение конуса по диаметру основания :  ΔAMB

OM - высота конуса   ⇒   ΔAMO - прямоугольный. Пусть ∠OMK=α

OK⊥AM  -  как радиус шара в точку касания с конусом  ⇒  ΔOKM - прямоугольный.  По отношению сторон прямоугольного треугольника :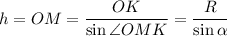 $h = OM = \dfrac{OK}{\sin \angle OMK}=\dfrac R{\sin\alpha }$

По отношению сторон прямоугольного треугольника ΔAMO:

$r = OA = OM\cdot tg \angle OMK=\dfrac R{\sin\alpha }\cdot \dfrac {\sin\alpha}{\cos\alpha }=\dfrac R{\cos\alpha}$

Тогда объём конуса по формуле

$V = \dfrac 13\cdot \pi r^2h=\dfrac { \pi}3 \cdot \dfrac{R^2}{\cos^2\alpha}\cdot \dfrac{R}{\sin\alpha}=\dfrac{\pi R^3}{3\cos^2\alpha~\sin\alpha}\\ \\ \\ V=\dfrac{\pi R^3}{3(1-\sin^2\alpha)\sin\alpha}=\dfrac{\pi R^3}{3(\sin\alpha-\sin^3\alpha)}$

Объём конуса, выраженный дробью, будет наименьшим, когда знаменатель будет наибольшим.

Наибольшее значение функции в знаменателе можно найти через производную.

f (α) = sin α - sin³ α    

f'(α) = (sin α - sin³ α)' = 0

cos α - 3 sin² α cos α = 0

cos α (1 - 3 sin²α) = 0

1) cos α = 0    ⇒    α = 90°  -  не подходит по условию  (угол при вершине сечения не может быть равен  180°).

1 - 3 sin²α = 0 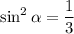   ⇒    $\sin^2\alpha =\dfrac 13$    ⇒

$\sin\alpha =\dfrac 1{\sqrt 3}$  - только положительное значение корня, так как отрицательным угол при вершине конуса быть не может.

Высота конуса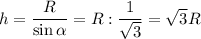  $h = \dfrac R{\sin\alpha }=R:\dfrac 1{\sqrt3}=\sqrt3R$

ответ: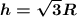  $\boldsymbol{h = \sqrt3R}$

=======================================

$f(\alpha) = \sin \alpha - \sin^3\alpha =\dfrac 1{\sqrt3}-\dfrac 1{3\sqrt3}=\dfrac 2{3\sqrt3}$

Наименьший объём описанного конуса с высотой  h=√3 R

$V =\dfrac{\pi R^3}{3(\sin\alpha-\sin^3\alpha)}=\dfrac{\pi R^3}{3\Big(\dfrac2{3\sqrt3}\Big)}=\dfrac{\sqrt3}2\cdot \pi R^3$