Номер 1.
1) (486 + 351) + 514 = (486 + 514) + 351 = 1000 + 351 = 1351
2) 2786 + 871 + 129 = (871 + 129) + 2786 = 1000 + 2786 = 3786
3) 147 + 256 + 353 + 244 = (147 + 353) + (256 + 244) = 500 + 500 = 1000
4) (3681 + 11 388) + (4319 + 1612) = (3681 + 4319) + (11 388 + 1612) =
= 8000 + 13 000 = 21 000
Номер 2.
1) (148 + 245) - 45 = (245 - 45) + 148 = 200 + 148 = 348
2) (473 + 132) - 173 = (473 - 173) + 132 = 300 + 132 = 432
3) 843 - (154 + 243) = (843 - 243) - 154 = 600 - 154 = 446
4) 894 - (394 + 148) = (894 - 394) - 148 = 500 - 148 = 352
Что мы будем использовать: последовательность 
монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
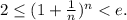
1) 
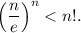При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 
Имеем:
2) 
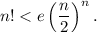При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что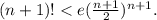 
Имеем:
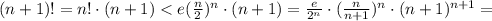
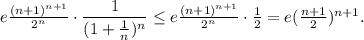
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).
