бесконечность
Пошаговое объяснение:
Вот смотри, тут решать особо и не надо.
Вот смотри, у тебя в числителе 2х^3+5, где 2 и (+5) не играет особой роли, в знаменателе та же история, только там х^2
Теперь обратим внимание на то, что есть формула
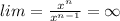
где х стремится к бесконечности. (если не преобразилась формула то там написано предел, х-> к бесконечности, в числителе х^n, в знаменателе x^(n-1) вообще не обязательно может быть минус 1, но как факт чстепень числителя больше степени знаменателя)
из этой формулы делаем вывод что ответ будет бесконечность.
Надеюсь, что все понятно объяснила, если да, то сделай лучшим
а) 128√2 *π см³
б) 64 π см²
Пошаговое объяснение:
Сначало нужно найти катет данного треугольника. Его мы находим по теор. Пифагора. А также данный треугольник является равнобедренным, значит два катета являются равными, а также их противоположные углы равны 45°. Значит √2а² = с. ⇒ а = 8 см
теперь можно и найти высоту данного прямоугольного треуг. В этом случае она будет делить треугольник на ровные две части. Полученные две части тоже будут прямоугольными треугольниками, а также их углы как и в начальном треугольнике равны 45°. Получается что половина гипотенузы равна и высоте начального треугольника h=c/2=4√2 cм
а) В этом случае нам нужно найти объем конуса. Радиус этого конуса будет равен половине гипотенузы ⇒ r=c/2=4√2 cм
Чтобы найти объем конуса нам нужно воспользоватся данной формулой ⇒ V=1/3 * h * S
Площадь нижней окружности можно вычислить по данной формуле S=πr²=( 4√2 )² * π = 32π cм²
V= 1/3 * 4√2 * 32π cм² = 128√2*π*/3 см³
б) Чтобы найти площадь полной поверх. конуса нужно по отдельности вычислить площадь боковой поверхности и площадь основания конуса.
Sбок= πrl=32π см²
Sосн=32π см²
Sпол= 32π + 32π = 64π см²
36 - 12- 16 = 8м^2