ответ:
пошаговое объяснение:
при умножении степеней с одинаковым основанием показатели складываются, а при делении отнимаются, ну и основание остаётся неизменным
с⁷+с³=с⁷⁺³=с¹¹ х⁸: х⁴=х⁸⁻⁴=х⁴
а³ а
х⁶ с⁵
и так далее, плохо видно
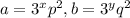, где p и q - натуральные числа, не делящиеся на 3. Ясно, что x<n, y<n. Если x=y, то, разделив обе части на 
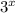, получим уравнение 
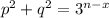. Поскольку числа p и q не делятся на 3, а величина n-x больше 0, это уравнение корней не имеет. Наконец, рассмотрим случай, когда x≠y, в силу симметрии можно считать, что x<y. Разделив уравнение на 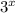, имеем 
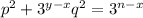. Первое слагаемое не делится на 3, второе и третье делятся, получили противоречие.
2) 40*8=320 (км) - такой путь они проехали на автобусе
3) 780-320 = 460 (км) - на столько больше проедут они на ж/д
ответ: на 460 км.