Первоначальные числа (3;9;27) или (27;9;3). Первая прогрессия возрастает, вторая - убывает.
Пошаговое объяснение:
Так как у нас геометрическая прогрессия, запишем условие в виде
b+b*q+b*q^2=39
также запишем условие для арифметической прогрессии
b+(b+k)+(b+2k)=39-12
упростим
3b+3k=27
b+k=9
для второго числа запишем его вид для арифметической и геометрической прогрессии
b+k=b*q
преобразуем
q=(b+k)/b или q^2=(b+k)^2/b^2
для третьего числа запишем его вид для арифметической и геометрической прогрессии
b+2k=b*q^2-12
q^2=(b+2k+12)/b
запишем выражение для q^2 из второго и третьего числа
(b^2+2*b*k+k^2)/b^2=(b+2k+12)/b
по правилу пропорции преобразуем
b^3+2*b^2*k+b*k^2=b^3+2*b^2*k+12*b^2
приведем подобные слагаемые и упростим
b*k^2=12*b^2
12b=k^2
выразим одну переменную через другую
b=9-k
и подставим в наше уравнение
108-12k-k^2=0
решим уравнение
k^2+12k-108=0
D=144+4*1*108=144+432=576
k=(-12+24)/2=6
k=(-12-24)/2=-18
для первого корня (k=6)
b=3 - первое число
b+k=9 - второе число
b+2k=15
q=3 - знаменатель геометрической прогрессии
b*q^2=27 - третье число
для второго корня
b=27 - первое число
b+k=9 - второе число
b+2k=-9
q=1/3 - знаменатель геометрической прогрессии
b*q^2=3
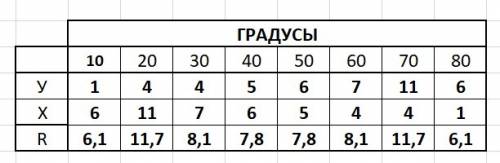
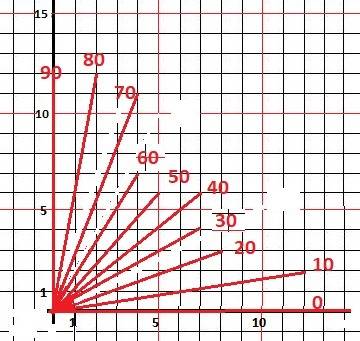
1) Берём транспортир и делаем рисунок до пересечения с узлом сетки - в приложении.
2) Заполняем таблицу с результатами измерений. Узел обозначаем точкой на рисунке и двумя координатами в таблице. Таблица в приложении. А на рисунке они не обозначены, чтобы их было видно.
3) Определить путь - измерить расстояние линейкой между этими точками и началом координат. Можно и вычислить по теореме Пифагора гипотенузу: c = √(x²+y²).
4) Сравнить результаты - отношения Х и У - обратные -
1/6 и 6/1, 4/11 и 11/4, а длины отрезков - равные.
5) Построить силой Разума угол примерно 30° - запросто - семь направо четыре вверх.
Дополнительно.
45° = 1/1.
3x^2-27=0
x^2-9=0
x1=3, x2=-3 (не принадлежит промежутку)
y(0)=0
y(3)=27-81=-54 (наименьшее)
y(4)=64-108=-44
2)y'=3x^2-6x
3x^2-6x=0
3x(x-2)=0
x1=0 (не принадлежит промежутку), x2=2
у(1)=1-3+2=0
у(2)=8-12+2=-2 (наименьшее)
у(4)=64-48+2=18
Перепроверьте на всякий случай