суммой двух векторов называется вектор,получаемый из начала первого вектора в конец второго. При этом второй вектор начинается в точке окончания первого вектора. Правило треугольника АВС вектор АВ начинается в А + вектор ВС вектор начинается в В и кончается в С. сумма этих векторов равна вектору АС.
a +b =c или AB+AD=AC
можно построить параллелограмм АВСД . по правилу сложения и тут получается тот же результат
Так как DC=AB=b , то a+b=AD+DC=AC=c , выполняя сложение по правилу треугольника, суммой остаётся тот же вектор c . Поэтому оба сложения равноценны.
1. Для любых двух векторов a и b выполняется равенство a+b =b +a (коммутативный или переместительный закон сложения).
2. Для любых трёх векторов a, b, c в силе равенство (a +b )+c=a+(b+c ) (ассоциативный или сочетательный закон сложения).
В решении.
Пошаговое объяснение:
Вопросы теме " Функции".
Для каждой из трех функций ( прямо пропорциональная зависимость, линейная, обратно пропорциональная зависимость, запишите:
1. формулу, задающую эту зависимость;
2. что является графиком данной функции;
3. нарисуйте график каждой функции;
4. как определить, проходит ли график через данную точку.
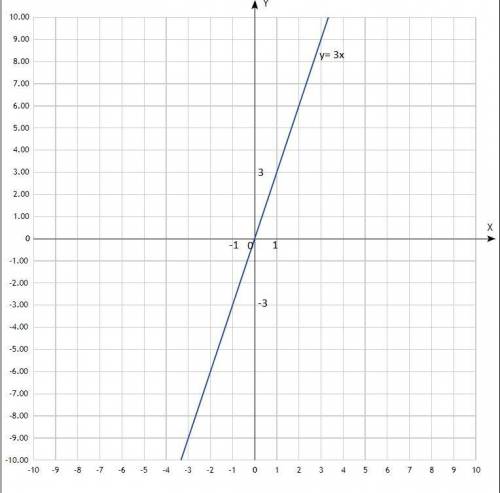
1) Прямо пропорциональная зависимость: у = kх; график - прямая, проходящая через начало координат.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3х;
Таблица:
х -1 0 1
у -3 0 3
По вычисленным точкам построить прямую.
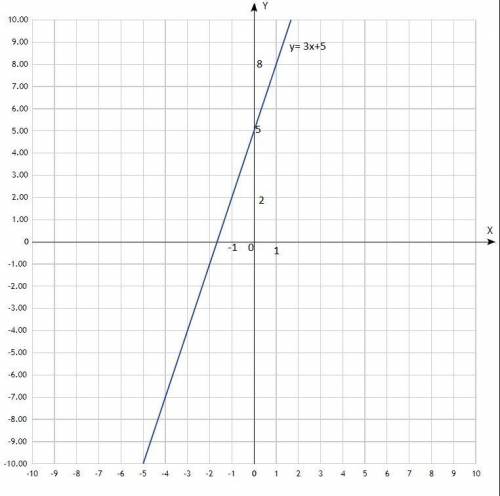
2) Линейная функция: у = kx + b; график - прямая линия.
Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 3х + 5;
Таблица:
х -1 0 1
у 2 5 8
По вычисленным точкам построить прямую.
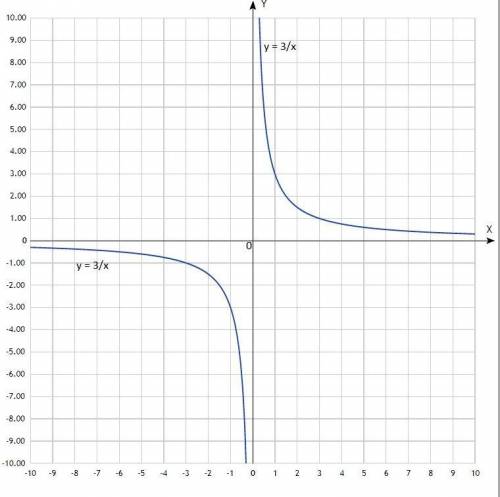
3) Обратно пропорциональная зависимость: у = k/x; график - гипербола, состоящая из двух ветвей.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = 3/х;
Таблица:
х -10 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 10
у -0,3 -0,5 -0,6 -0,75 -1 -1,5 -3 - 3 1,5 1 0,75 0,6 0,5 0,3
По вычисленным точкам построить гиперболу.
4) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
По условию площадь прямоугольника равна 12 см², тогда стороны должны быть такими, чтобы
а·в = 12
Варианты:
1·12 = 12
2·6 = 12
3·4 = 12
Поэтому можно построить несколько прямоугольников с такой площадью:
1) а = 1 см; в = 12 см
2) а = 2 см; в = 6 см
3) а = 3 см; в = 4 см