1 - 1 кг(40%), 2- 2кг(60%).
Пошаговое объяснение:
Пусть x - масса 1-ого раствора, у - масса 2-ого раствора, тогда x+y масса смеси этих двух растворов. Выразим массу соли в этих растворах:
0,4х - масса соли в 1-ом растворе.
0,6у - масса соли в 2-ом растворе.
0,4х + 0,6 у - масса соли в смеси.
Найдём концентрацию в смеси, для этого разделим массу соли на массу смеси растворов.
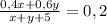
Это уравнение составлено по 1-ому условию. Теперь составим уравнение по второму условию.
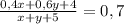
Теперь мы получили систему уравнений, решим ей и найдём ей корни.
Для начала выразим из 1-ого выражения x, а затем подставим его во 2-ое.
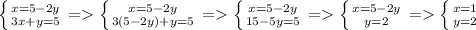
Значит масса 1-ого раствора - 1 кг, а 2-ого - 2 кг.
Проверка:
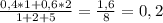
и
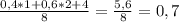
1. преобразуем правую часть. 3*(1-sin²x)-2sinx+1= 3*1-sin²x-2sinx+1=
4-sin²x-2sinx=-(sinx+1)²+5
Наибольшее значение эта сумма принимает, когда скобка равна нулю. и сумма эта равна 5, а наименьшее, когда синус равен 1, а сумма 5-4=1.
2. (х²+(3b-1)*x+2b²-2)/(x²-3x-4); По Виету знаменатель обращается нуль при х=-1 и х=4, исключим их из ОДЗ, х≠-1; х≠4.
дробь равна нулю. когда знаменатель отличен от нуля, а числитель равен нулю.
ровно одно решение, или два одинаковых, дискриминант равен нулю. В вашем случае дискриминант равен нулю, если (3b-1)²-8b²+8=0;
9b²-8b²-6b+1+8=0; b ²-6b+9=(b-3)²=0, т.е. b=3.
Проверим при b=3.
(х²+8х+18-2)/(х²-3х-4)=0, (х-4)²=0; х=4; но он не входит в область определения.
Возьмем теперь корни, при которых знаменатель обращается в нуль. т.е. х=-1,
1-3b+1+2b²-2=0, тогда 2b²-3b=0⇒b=0 или b=1.5
Проверим при b=0; х²-х-2=0, один корень равен -1, но он не входит в ОДЗ, зато второй х=2 и он единственный. При а=1.5 получаем х²+3.5х+1=0; х=(-3.5±1.5)/2; х=-2, х=-1- не входит в ОДЗ,
и при х=4, получим 16+12b-4+2b²-2=0; 2b²+12в+10=0; b²+6в+5=0; По Виету b=-1; b=-5; проверим
х²-4x+2-2=0, (х-4)*х=0, корни х=4- не входит в ОДЗ и х=0подходит.
проверим b=-5
х²-16х+50-2=0;х²-16х+48=0 По Виету х=4, - лишний, х=12, подходит.
ответ b=0; b =1.5; b=-1; b=-5
1)7772-134%
х-100%
х=7772*100/134
х=5800
2) 800-100%
1096-х
х=1096*100/800
х=137