ответ: x = ± 5.
Дано: x⁴ - 10*x³ + 250*x - 625 = 0.
Пошаговое объяснение:
Применим теорему Безу, по которой свободный член полинома = -625 - произведение корней уравнения.
Эта теорема выглядит так.
x₁ * x₂ * x₃ * x₄ = - 625 = - 5⁴
Можно предположить, что два корня действительные: +/- 5.
(x -5) * (x+ 5) * (х -x₃) * (х- x₄) = 0
Проверим это делением многочленов - разделим сразу на : (х² - 25)
Расчет на рисунке в приложении.
Разделилось без остатка и получили в результате
x² - 10*x + 25 = (х - 5)² = 0
Решаем это квадратное уравнение и получаем еще два корня: х = 5
Должно получиться: (x-5)³*(x+5) = 0.
В подтверждение расчёта - график функции - в приложении.
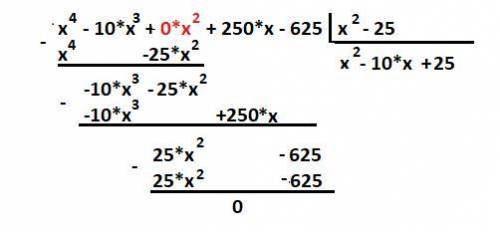
Цитаты: "Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). Линейный угол - это угол, образованный пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней.
АВ- двугранный угол, точка М удалена от плоскостей на расстояние m, то есть МС=МD=m. DК и CK перпендикулярны AB (теорема о трех перпендикулярах). <DKC- линейный угол данного нам двугранного угла, равного 120*. Проведем МК. Поскольку точка М равноудалена от сторон угла DKC, МК - биссектриса этого угла и <МКС=120° /2=60°.
В прямоугольном треугольнике КМС <MKC=60*, значит <KМC=30°. Следовательно КМ=2КС и по Пифагору 4КС²-КС²=m². Тогда КС=m/√3.
Поскольку МК=2КС , МК=2m/√3 или МК=2m√3/3.
Не очень уверена!