Решите : в вазе лежало 32 яблока и 8 груш. во сколько раз больше лежит яблок, чем груш? напишите, , с решением?

👇

Увидеть ответ

Ответ:

LeraKruspe

10.03.2023

1)32:8=4
Відповідь: в 4 рази

4,4(62 оценок)

Ответ:

Dalishka808

10.03.2023

32:8=4 раза - яблок больше, чем груш

4,4(88 оценок)

Открыть все ответы

Ответ:

nastya01241

10.03.2023

Пусть x км составляет весь маршрут
0,25x км - 25% всего маршрута
(0,25x+15) км - проехал за I день
x-(0,25x+15)=x-0,25x-15=0,75x-15 (км) - остаток
(0,75x-15)*0,2=0,15x-3 (км) - 20% остатка
0,15x-3+48=0,15x+45 (км) - проехал за II день
x-(0,25x+15+0,15x+45)=x-0,4x-60=0,6x-60 (км) - остаток пути после двух дней
(0,6x-60):2=0,3x-30 (км) - половина оставшегося пути
0,3x-30+20=0,3x-10 (км) - проехал за III день
220 км - IV день
Составим уравнение:
(0,25x+15)+(0,15x+45)+(0,3x-10)+220=x
0,7x+270=x
x-0,7x=270
0,3x=270
x=270:0,3
x=900 (км) - весь маршрут

ответ: 900 км

4,4(26 оценок)

Ответ:

evasauteeva

10.03.2023

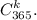
Пусть девочек n, а мальчиков m=n+12. Найдем вероятность того, что ни в одной паре мальчик-девочка нет одинаковых дней рождения. Рассмотрим множество всех 365 дней в году. Выберем произвольный набор из k дней в году и найдем количество которыми можно распределить дни рождения всех n девочек по дням этого набора (k=1,...,n). Кстати, количество таких наборов равно $\displaystyle C_{365}^k.$

Количество которыми можно разбить n-элементное множество на k непустых подмножеств выражается числом Стирлинга второго рода, которое обозначается S(n,k) (порядок следования получающихся подмножеств не учитывается). Легко понять, что S(n,n)=1, S(n,1)=1 и для n≥3 и 2≤k<n верна рекуррентная формула S(n,k)=S(n-1,k-1)+kS(n-1,k). Действительно, зафиксируем n-1 элементов n-элементного множества. Тогда эти n-1 элементов можно разбить на k-1 подмножеств и добавить подмножество состоящее из одного n-го элемента. Это даст получить k подмножеств n-элементного множества. Кроме того, из каждого разбиения тех фиксированных n-1 элементов, на k подмножеств, добавляя к каждому подмножеству разбиения n-ый элемент, мы получаем еще k разбиений n-элементного множества. Таким образом, числа Стирлинга второго рода можно вычислять по аналогии с треугольником Паскаля:
n=1: [1]
n=2: [1,1]
n=3: [1,3,1]
n=4: [1,7,6,1]
n=5: [1,15,25,10,1]
n=6: [1,31,90,65,15,1]
n=7: [1,63,301,350,140,21,1]
n=8: [1,127,966,1701,1050,266,28,1]
n=9: [1,255,3025,7770,6951,2646,462,36,1]
n=10: [1,511,9330,34105,42525,22827,5880,750,45,1]
n=11: [1,1023,28501,145750,246730,179487,63987,11880,1155,55,1]

Итак, множество всех девочек можно распределить по k фиксированным дням Здесь появился k!, т.к. подмножества получаемых разбиений можно переставлять по k дням этого набора (напомню в S(n,k) получаемые подмножества не упорядочены). Для каждого такого распределения девочек по k фиксированным дням года, дни рождения m мальчиков распределяются по остальным дням года (365-k)^m

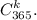Т.к. количество наборов по k дней равно $\displaystyle C_{365}^k.$ и k меняется от 1 до n, то общее количество распределить n девочек и m мальчиков по дням года так, чтобы д.р. мальчиков не совпадали с д.р. девочек равно 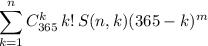$\displaystyle\sum\limits_{k=1}^nC_{365}^k\, k!\,S(n,k)(365-k)^m$ или, что то же самое, 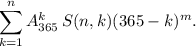$\displaystyle\sum\limits_{k=1}^nA_{365}^k\,S(n,k)(365-k)^m.$ Т.к. 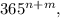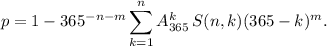количество всех распределить n+m детей по дням года равно $365^{n+m},$ то $p=1-365^{-n-m}\displaystyle\sum\limits_{k=1}^nA_{365}^k\,S(n,k)(365-k)^m.$
Вычисляем это при n=1,2,3,....,11 c учетом того, что m=12+n:
p1 = 0,035036804...
p2 = 0,073939488...
p3 = 0,116134389...
p4 = 0,161019616...
p5 = 0,207979214...
p6 = 0,256397031...
p7 = 0,305669832...
p8 = 0,355219316...
p9 = 0,404502689...
p10 = 0,453021579...
p11 = 0,500329116...
Как видно, первый раз вероятность превысит 0,5 при n=11 т.е. общее количество детей в этом случае равно 11+(11+12)=34.

4,7(25 оценок)

Это интересно:

Образование

27.04.2022

Первые 300 км автомобиль ехал со скоростью 60 км/час...

Образование

02.06.2023

В треугольнике АВС точка D на стороне АВ...

Образование

21.07.2020

Из разных городов, расстояние между которыми 600 км...

Образование