ответ: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Пусть пуд сахара стоит х, а фунт чая - y. Тогда можем составить и решить такую систему уравнений:
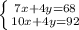
Решаем систему методом вычитания (находим x):
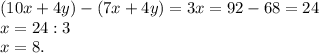
Теперь можно найти y:
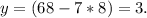
Итого: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Задачу можно решить и арифметически, заметив, что и там, и там по 4 фунта чаю:
1). 92 - 68 = 24 (рубля) - разница между 7 пулами и 10 пудами сахара.
2). 10 - 7 = 3 (пуда) - разница между 7 пудами и 10 пудами сахара.
3). 24 : 3 = 8 (рублей) - стоит пуд сахара.
4). (68 - 8 * 7) : 4 = 3 (рубля) - стоит фунт сахара.
Так как на мотете может выпасть орёл или герб, а всего монет три, то всего возможно вариантов 23 = 8. Возможные варианты выпадений:
1) О О О;
2) О О Р;
3) О Р О;
4) О Р Р;
5) Р О О;
6) Р О Р;
7) Р Р О;
8) Р Р Р;
Где Р – решка (герб), О – орёл.
Условию, что только на одной монете выпадет герб, удовлетворяют 3 случая: (2), (3), (5).
Чтобы найти вероятность, что герб выпадет только на одной монете, необходимо разделить благоприятные исходы на общее число исходов:
P = 3/8 = 0,375.
ответ: 0,375.
Условию, что на всех монетах выпадет герб, удовлетворяет 1 случай: (8).
Чтобы найти вероятность, что герб выпадет на всех монетах, необходимо разделить благоприятные исходы на общее число исходов:
P = 1/8 = 0,125.
ответ: 0,125.
Условию, что герб выпадет хотя бы на одной монете, удовлетворяет 7 случаев: с (2) по (8).
Чтобы найти вероятность, что герб выпадет хотя бы на одной монете, необходимо разделить благоприятные исходы на общее число исходов:
P = 7/8 = 0,875.
ответ: 0,875.
Условию, что герб выпадет не менее, чем на двух монетах, удовлетворяют 4 случая: (4), (6), (7), (8).
Чтобы найти вероятность, что герб выпадет не менее, чем на двух монетах, необходимо разделить благоприятные исходы на общее число исходов:
P = 4/8 = 0,5.
ответ: 0,5.
4 2/7 : 3 3/4 = 30/7 : 15/4=30/7*4/15=2/7*4/1=8/7=1 1/7
1 - (1/10 + 3/5) = 1-(1/10-6/10)=1-(-5/10)=1-(-1/2)=1+1/2=1 1/2