Пошаговое объяснение:
I вариант решения
пусть прямая симметричная прямой y=-2x+3 имеет вид у=kx+b
найдем точки пересечения прямой y=-2x+3 с осями координат относительно оси ОУ
с осью ОХ у=0; -2x+3=0; 2x=3; x=1,5; (1,5;0)
с осью ОY x=0; y=3; (0;3)
так как прямые симметричны то
- они обе проходят через точку (0;3)
- симметричная прямая проходит через точку противоположную точке (1,5;0) точку (-1,5;0)
⇒ симметричная прямая проходит через точки (0;3) и (-1,5;0)
подставим координаты точки (0;3) в уравнение симметричной прямой у=kx+b координату точки (0;3)
получим 3=к*0+b; b=3
подставим координаты точки (-1,5;0) и значение b=3 в уравнение симметричной прямой у=kx+b получим
0=-1,5к+3 ; 1,5к=3; k=3/1,5=2
подставим b=1; k=2 в уравнение у=kx+b
у=2х+3
===============================================
II вариант решения - тригонометрический
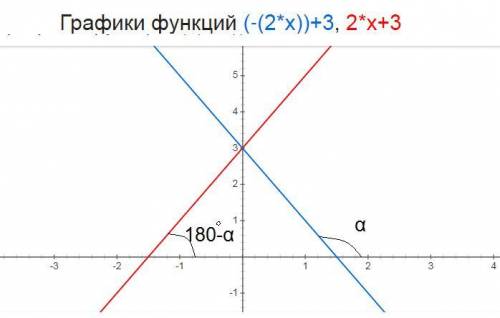
так как прямые симметричны то их углы наклона к оси ОХ будут в сумме давать 180°
так как tg(180°-а)=-tga то угловые коэффициенты симметричных прямых будут к₁ и к₂ противоположными числами а значение b₁ и b₂ будут одинаковыми так как обе прямые пересекают ось ОУ в одной точке ⇒ к₂=-к₁=-(-2)=2; b₂=b₁=3
уравнение прямой симметричной прямой y=-2x+3 относительно оси ОУ
у=2х+3
var
a,b,c,x,y:real;
begin
Write('Введите a и b: '); Read(a,b);
repeat
Write('Введите c, не равное нулю: ');
Read(c)
until c<>0;
x:=2*sqr(a)-b/(3*c);
{
Если Вы относитесь к людям, ненавидящим скобки
и тех, кто решает Ваши задания, то в Вашем условии
на 3а делится все выражение, и тогда предыдущая строка
должна иметь вид x:=(2*sqr(a)-b)/(3*a);
}
if x>=0 then
begin y:=sqrt(x+sqr(c))+4*a*b; Writeln('x=',x,', y=',y) end
else
Writeln('x=',x,', y вычислить нельзя, под корнем отрицательное значение')
end.
Тестовое решение:
Введите a и b: 3.4 -2.18
Введите c, не равное нулю: 0
Введите c, не равное нулю: 5.172
x=23.2605001288992, y=-22.5762191684909
Обозначают так: точка отсчета, начало луча, к примеру А, вторая буква - это ближе к концу графического изображения луча, к примеру В. Луч АВ.
2.Углом называется часть плоскости ограниченная двумя лучами.
Сами лучи называются сторонами угла, а общая точка, из которой лучи выходят, называются вершиной угла.
3.Градусная мера, которого 180 градусов.