Потому что, если построить график функции y = xˣ :
x xˣ
0,9 0,909
0,8 0,836
0,7 0,779
0,6 0,736
0,5 0,707
0,4 0,693
0,3 0,697
0,2 0,725
0,1 0,794
0,01 0,955
0,001 0,993
0,00001 0,9998
то легко заметить, что поначалу значения уменьшаются. Чем больше x - тем больше xˣ, и наоборот. Но, по мере приближения к нулю, примерно в районе 0.3, внезапно, значения xˣ начинают расти, и чем меньше х, тем х в степени х ближе к единице. Поэтому логично предложить, для непрерывности, что и в самой точке 0 выражение строго равно 1.
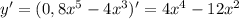
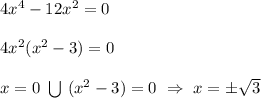
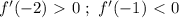
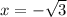производная меняет знак с "+" на "-" значит это точка максимума.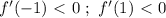
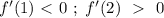
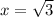производная меняет знак с "-" на "+" значит это точка минимума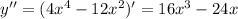
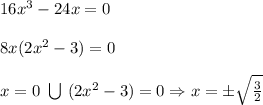
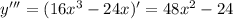
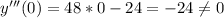
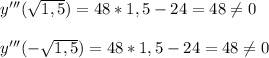
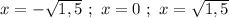функция имеет перегиб.
х - количество пирожков
1/2х - продал до матча
1/2х - остаётся продать = 7/7 остатка
2/7х - остаётся не проданным, значит всего продано 5/7х пирожков
5/7х = 1/2х + 15
5/7х - 1/2х = 15
10/14х - 7/14х = 15
3/14х = 15
Находим целое по его части: 15 : 3 * 14 = 70 (пирожков) было первоначально
Проверка: 1/2 * 70 = 35 пирожков (до матча) + 15 пирожков (в перерыв) + 2/7 * 70 = 70 : 7 * 2 = 20 пирожков (осталось).
35 + 15 + 20 = 70 пирожков