Question

По вероятности❤️из трех колод карт (по 36) случайным образом вынимается по одной карте. найти вероятность того, что среди вынутых карт по крайней мере 2 окажутся бубновой масти.

Answer 1

Пошаговое объяснение:

Вероятность, что из одной колоды вынем бубновую карту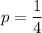 $p = \dfrac{1}{4}$.

Вероятность, что вынем ровно 2 бубновые карты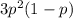 $3 p^2 (1 - p)$, тройка здесь обусловлена тем, что у нас есть три возможных варианта выбрать колоду, из которой не выпадет бубновая карта

Вероятность, что вынем ровно 3 бубновые карты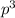 $p^3$

Итого: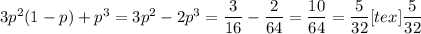 $3p^2(1- p) + p^3 = 3p^2 - 2p^3 = \dfrac{3}{16} - \dfrac{2}{64} = \dfrac{10}{64} = \dfrac{5}{32}<img src=$" alt="\dfrac{5}{32}" />" />