Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .
Находим векторы АВ, АС и АД.
Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.
Вектор АC={xC-xA, yC-yA, zC-zA} = (-6; 3; -4) =√61 ≈ 7,81025.
Вектор АD={xD-xA, yD-yA, zD-zA} = (-6; -1; -2) = √41 ≈ 6,40312.
Определяем векторное произведение АВ х АС.
i j k | I j
-4 2 -1 | -4 2
-6 3 -4 | -6 3 = -8i + 6j - 12k - 16j + 3i + 12k = -5i - 10j = (-5; -10; 0).
Далее находим смешанное произведение (АВ х АС) х АД.
(АВ х АС) = (-5; -10; 0),
АD = (-6; -1; -2),
(АВ х АС) х АД = 30 + 10 + 0 = 40.
Объем пирамиды равен (1/6) этого произведения:
V = (1/6)*40 = (20/3) куб.ед.
Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).
Площадь основания АВС равна половине модуля векторного произведения АВ х АС.
S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.
h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.
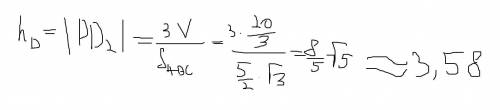
номер1
Пошаговое объяснение:
а)0 б)2 в)22 г)-18 д)7 е)-18 ж)18 з)-1
номер2
45+(-37)=8
-27+(-37)=-64
100+(-37)=63
номер3
а),б),в)
номер4
а)-134+156>-256+145
б)-76+(-108)<-58+(-135)
в)266+(-73)=-52+245
номер5
а)-520+600>0
б)-300+260<0
в)14+(-11)>0
г)-7+15=8
д)56+(-72)<10
е)-29+(-44)<-67
номер6
а)450+340=790
б)235+(-120)=115
в)-720+140=-580
г)-635+(-100)=-735
д)-450+340=-110
е)-235+(-120)=-355
ж)720+(-140)=580
з)-635+100=535
и)-450+(-340)=-790
к)-235+120=-115
л)720+140=960
м)635+(-100)=535
н)450+(-340)=110
о)235+120=355
п)-720+(-140)=-860
р)635+100=735
номер7
а)х-18=-25
х=-25+18
х=-7
ответ:7
б)4х-15=-12
4х=-12+15
4х=3
в)3х-35=-10
3х=-10+35
3х=25
х=8,3
номер9
а)-15+17+(-51)+93+(-78)=-34
б)45+(-13)+(-384)+15+(-492)=-507
в)47+(-8)+(-23)+(-9)+(-17)+23+34=-31
номер10
а)-48+(-212)+(-756))=-1016
б)(-57)+(-148))+(-505)=-707
в)(345+(-266))+(-75)=4