в первом 34 певца, во втором 36 певцов
Пошаговое объяснение:
т.к. 7/17 первого хора, то количество певцов в нем делится на 17
до 70 таких чисел 4: 17, 34, 51, 68
количество певцов во втором делится на 9
пусть в первом хоре 17х человек, а во втором 9у человек, по условию:
17х + 9у = 70
проверим х от 1 до 4
1) х = 1
9у = 70 - 17 = 53
53 не делится на 9
2) х = 2
9у = 70 - 34 = 36
у = 4 - решение
3) х = 3
9у = 70 - 51 = 19
19 не делится на 9
4) х = 4
9у = 70 - 68 = 2
2 не делится на 9
единственный вариант, который подходит: в первом 34, во втором 36
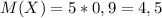, то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
Пошаговое объяснение:
Пусть проводится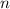 
независимых испытаний, даже не обязательно повторных. И в каждом из которых случайное событие 
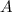может появиться с вероятностью 
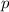. Тогда случайная величина 
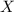, это число появлений события 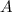в данной серии испытаний, имеет биномиальное распределение.
Кондрат последовательно заходит в 5 автобусов, то есть совершается серия и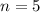 
и только 5 похождений в различные автобусы, где вероятность встретить контролера в каждом из них составляет 
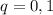. Тогда вероятность НЕ встретить контролера в автобусе равна 
.
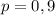Математическое ожидание при биномиальном распределении рассчитывается согласно формуле:
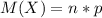, где 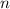- количество независимых испытаний, то есть количество автобусов, в которое последовательно заходит Кондрат, 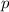- вероятность появления события 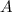, то есть автобуса без контролера.
Найдем математическое ожидание числа автобусов в которые успеет зайти Кондрат:
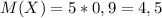- то есть среднеожидаемое количество автобусов, которое успеет посетить Кондрат.
Sn = 210 тонн - сумма n членов прогрессии
a₁ = 2 тонн -первый член арифметической прогрессии
n = 14 - число членов арифметич. прогрессии
an - энный член арифметич прогрессии
a₉ = ?
Sn = 1/2(a₁+ an)×n - используя эту формулу найдем a₁₄
210 = 1/2(2+an)×14
an = 210×2÷14-2
an = 210÷7-2
an =28
an = a₁ + d(n-1) - используя эту формулу найдем d -разность арифметической прогрессии
d =(an - a₁)÷(n-1)
d =(28-2)÷(14-1)
d = 26÷13
d = 2
a₉ = a₁ +d(n-1) - определим a₉
a₉ = 2 + 2 ×(9-1)
а₉ = 18