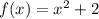 определена на множестве E
определена на множестве E 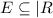
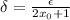 где
где 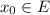 .
. на области
на области 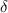 от
от  (то есть:
(то есть: 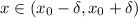 ) выполняется
) выполняется 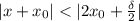 .
.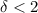 , выполняется
, выполняется 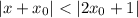 .
.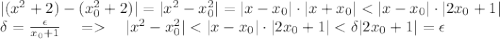
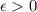 есть
есть 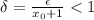 , на области которой выполняется
, на области которой выполняется 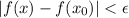
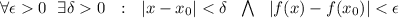 ). Следовательно -
). Следовательно - 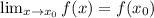 .
.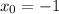 нужно отдельно доказать предел
нужно отдельно доказать предел 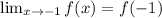 .
. . Но! Множество натуральных чисел
. Но! Множество натуральных чисел 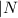 тоже подмножество
тоже подмножество  , значит
, значит 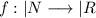 тоже непрерывна, получается - доказали что
тоже непрерывна, получается - доказали что 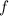 непрерывна на области определения? Известно, что
непрерывна на области определения? Известно, что 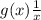 тоже непрерывна на области определения, но
тоже непрерывна на области определения, но 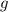 , понятное дело, не определена на
, понятное дело, не определена на  !
! " или, "непрерывна на отрезке
" или, "непрерывна на отрезке 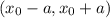 "...
"...
Повторные испытания с двумя исходами.
Вероятность найти арбуз весом не менее 10 кг равна
p=1/100=0,1
Вероятность не найти такой арбуз
q=1-p=1-0,1=0,9
По формуле Бернулли:
P₁₀₀₀(3)=C³₁₀₀₀0,1³·0,9⁹⁹⁷
Ясно, что нереально считать C³₁₀₀₀ и 0,9⁹⁹⁷
Поскольку
n=1000 - велико,
p=0,1 - мало
Применяем формулу Лапласа
np=1000·0,1=100
npq=1000·0,1·0,9=100·0,9=90
√npq=√90≈9,5
x=(3-100)/9,5
φ(-x)=φ(x)
Значения φ(x) находят по таблице.
φ(5)=0,0000015 ( и то очень маленькое).
P₁₀₀₀(3)≈0,0000015 /9,5=0,00000015789