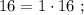
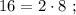
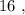т.е.: 
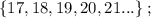
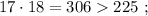
каждое – будет, очевидно, больше чем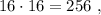 
т.е. больше 
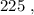а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.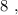
т.е.: 
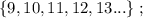
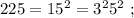
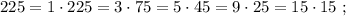
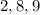и 
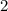и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы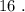 
и никаких натуральных чисел нет. и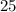 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы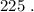 
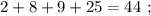
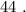
если разбирать комбинации выпадающих очков,то:
1- не выпадает
2 - 1\1 (1комб)
3-1\2: 2\1(2комб)
4-1\3: 2\2: 3\1(3)
5-1\4: 2\3; 3\2: 4\1 (4)
6-1\5: 2\4: 3\3: 4\2: 5\1(5)
7-1\6: 2\5: 3\4: 4\3: 5\2: 6\1(6)
8-2\6: 3\5: 4\4: 5\3: 6\2(5)
дальше до 12 идет к уменьшению комбинаций
Таким образом,можно утверждать,что чем больше возможных комбинаций выпадания очков,тем большая вероятность того,что выпадет именно это очко