1)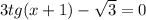
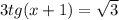
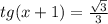
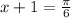
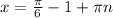
2)
3sin^2x+sinx*cosx-2cos^2x=0
Теперь делим все этоуравнение на cos^2x, получится:
3tg^2x + tgx - 2 = 0
tgx можно заменить на а(так легче решать просто):
tgx = a
3a^2 + a -2 = 0
И решаем квадратное уравнение:
D = 1^2 + 24 = 25
a1,2 = ( -1 +- 5 ) / 6 = > a1 = 2/3, a2 = -1 (эти числа подходят, т.к в тригонометрии промежуток идет от - 1 до 1, эти числа входят в этот промежуток)
Теперь, т.к мы делали замену tgx = a, то подставляем числа;
tgx = 2/3 => x = П/4 + Пn
tgx = -1 => x = arctg2/3 + Пn
1)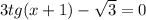
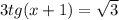
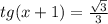
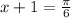
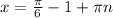
2)
3sin^2x+sinx*cosx-2cos^2x=0
Теперь делим все этоуравнение на cos^2x, получится:
3tg^2x + tgx - 2 = 0
tgx можно заменить на а(так легче решать просто):
tgx = a
3a^2 + a -2 = 0
И решаем квадратное уравнение:
D = 1^2 + 24 = 25
a1,2 = ( -1 +- 5 ) / 6 = > a1 = 2/3, a2 = -1 (эти числа подходят, т.к в тригонометрии промежуток идет от - 1 до 1, эти числа входят в этот промежуток)
Теперь, т.к мы делали замену tgx = a, то подставляем числа;
tgx = 2/3 => x = П/4 + Пn
tgx = -1 => x = arctg2/3 + Пn
1) Построим обычный известный график функции y=sinx (черный график на рис.)
2) Изменение аргумента означает параллельный перенос графика вдоль оси Ох. Т.к. стоит знак минус (x-π/2) - обозначает, что перенос графика нужно делать вправо на π/2. Получим функцию y=sin(x-π/2) (зеленый график на рис.)
3) Изменение значения функции означает параллельный перенос графика вдоль оси Оу. Т.к. стоит знак плюс, то сдвиг производим вверх на 1 единицу. Получаем график функции y=sin(x-π/2)+1 (синий график на рис.)