Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 - 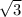
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
Пошаговое объяснение:
410860 + м * 20 = 489000;
м * 20 = 489000 - 410860;
м * 20 = 78140;
Для того, чтоб найти неизвестный множитель необходимо произведение разделить на известный множитель:
м = 78140 : 20;
м = 3907.
Проверка. Проверка необходима для того, чтоб проверить правильно ли найдено значение переменной. Если правая и левая часть равны, значит корень уравнения найден верно.
410860 + 3907 * 20 = 489000;
410860 + 78140 = 489000;
489000 = 489000.
ответ: 3907.
75880:(n-29965)=70
n-29965=75880:70
n-29965=1084
n=1084+29965
n=31049
ответ:т=31049.
2Y = 5 - X
Y = 2,5 - 0,5X
Y^2 = ( 2,5 - 0,5X)^2 = 6,25 - 2,5X + 0,25X^2
2X^2 + Y^2 - XY + X = 5
2X^2 + 0,25X^2 - 2,5X + 6,25 - X * ( 2,5 - 0,5X) + X = 5
2,25X^2 - 2,5X + 6,25 - 2,5X + 0,5X^2 + X = 5
2,75X^2 - 4X + 1,25 = 0
D = 16 - 13,75 = 2,25 ; √ D = 1,5
X1 = ( 4 + 1,5 ) : 5,5 = 1
X2 = 2,5 : 5,5 = 5/2 : 11/2 = 5/11
Y = 2,5 - 0,5X
Y1 = 2,5 - 0,5 = 2
Y2 = 2,5 - (1/2 * 5/11) = 2,5 - ( 5/22) = 5/2 - 5/22 = 55/22 - 5/22 = 50/22 = 25/11 =
= 2 целых 3/11
ответ : ( 1 ; 2 ) U ( 5/11 ; 2 3/11 )