1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Нет деления на ноль.
2. Пересечение с осью Х. Y= x²*(x+9) при х = 0,0, 9
Положительна - во всем интервале..
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = -∞
Горизонтальной асимптоты - нет.
5. Исследование на чётность.Y(-x) ≠ - Y(x).
Функция ни чётная ни нечётная - общего вида.
6. Производная функции.Y'(x)= -3*x² +18*х = -3*х*(x-6).
Корни при Х= 0 и 6.
(-∞)__(<0-убыв)__(0)___(>0-возр)___(6)__(<0-убыв)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(6)= 108 , минимум – Ymin(0)=0.
8. Интервалы возрастания и убывания.
Возрастает - между корнями - Х∈[0;6], убывает = Х∈(-∞;0]∪[6;+∞).
8. Вторая производная - Y"(x) = -6*x + 18= -6*(х -3)=0.
Корень производной - точка перегиба Y"(x)= 0 при х=3.
9. Выпуклая “горка» Х∈(3;+∞), Вогнутая – «ложка» Х∈(-∞;3).
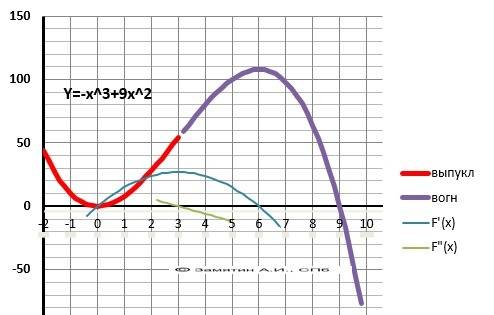
10. График в приложении.
ответ: х₁=1, х₂=2; х₃=n/2, если n=2; 3;4.
Пошаговое объяснение:1) Сначала найдём ОДЗ: подкореноое выражение должно быть неотрицательно, т.е. 3х - х² - 2 ≥ 0 ⇔ х²-3х + 2 ≤ 0. Через дискриминант Д = 9 - 8=1 или по т. Виета х₁=1, х₂=2; функция у=х²-3х + 2 ≤ 0 на [1; 2] ОДЗ: х∈ [1; 2] 2) Уравнение представляет из себя произведение двух множителей, оно равно нулю, если хотя бы один из множителей равен нулю, т.е. √(3х-х²-2) =0 или Sin 2πх=0 ⇒ а) 3х-х²-2 =0 х₁=1, х₂=2 б) 2πх=nπ, где n∈Z, х₃= nπ/(2π)=n/2, n∈Z 3) Корни х₁=1, х₂=2 удовлетворяют ОДЗ, х₃=n/2 удовлетворяет ОДЗ, если n=2; 3;4.