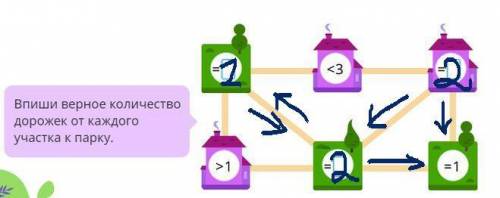
У нас шесть парков, условно обозначим их цифрами от одного до шести. Первый, третий и пятый парки у нас без числовых обозначений: будем туда их вписывать.
Парк номер один - в левом верхнем углу - к центральному нижнему (пятому) имеет лишь одну дорожку. В первый парк вписываем цифру один.
От пятого парка - внизу в центре - будут отходить уже две дорожки, потому что одна пойдет направо в шестой, а вторая реверсом в первый парк. В пятый парк вписываем цифру два.
От третьего парка (в правом верхнем углу) также прокладываются две дорожки, одна из которых идет к шестому (прям под ним), а вторая - по диагонали к пятому. В третий парк записываем двоечку.
Пусть искомая сторона, лежащая против тупого угла, равна х. Тогда х - четное число, по условию, и x>12, как сторона, лежащая против большего угла. С другой стороны x<18, суммы двух других сторон. Поэтому возможны два решения: х=14 или х=16. Это подтверждается и теоремой косинусов:квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
196=36+144+16, 256=36+144+76, следовательно, косинус противолежащего угла отрицательный, значит угол больше прямого.
ответ: 14 или 16.
480/800=0,6
320/800=0,4
100*0,6=60 м кв площадь первого
100*0,4=40 м кв - второго