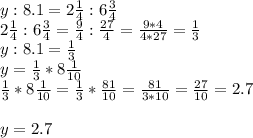
Пошаговое объяснение:
Монета брошена шесть раз.
В результате одного броска выпадет О или Р (Орел или Решка) с равной вероятностью 0,5.
Если записать результат 6 бросков, то получим цепочку, состоящую из 6 символов О или Р.
Например, исход - цепочка ООРОРО означает, что первый раз выпал Орел,
второй раз - Орел, третий раз - Решка и т.д..
Так как при каждом броске имеем 2 варианта (О или Р), а бросков 6,
то всего исходов (цепочек) имеем 26= 64. (В общем случае при n бросках имеем 2n исходов).
Пусть событие А = "Орел выпадет не менее трех раз" (3 или больше 3-х раз).
Противоположное событие (не А) = "Орел выпадет 1 раз, 2 раза или ни разу".
Подсчитаем количество исходов, при которых в цепочке
Орел будет встречаться 0, 1 или 2 раза.
- 1 исход (Орел не выпал ни разу)
Р, ОР, ООРООО, ОООРОО, РО, Р. 6 исходов
С62 = 6!/(2!*4!) = 6*5/2=15 исходов, (
Всего благоприятных исходов (орел выпал более двух раз, т.е. не менее трех)
64 - (1+6+15) = 42.
Р = 42/64 = 0,65625
можно, только если эти квадраты будут разными
Пошаговое объяснение:
1) Если имеется ввиду что два квадрата будут иметь одинаковую площадь.
Для этого нужно вычислить площадь квадрата, разделить ее на 2 и извлечь корень, чтобы узнать длину стороны квадрата с такой площадью.
15²=225 см² 225/2=112,5 √112,5≈10,6 (не целое)
26²=676 см² 676/2=338 √338≈18,4 (не целое)
Значит и для 15 см и для 26 см - нельзя.
2) Если размер квадратов произвольный, то нужно разложить площади исходных квадратов на сумму двух площадей, которые являются квадратами целых чисел (квадраты берем из "Таблицы квадратов чисел").
225=81+144 =9²+12² (т.е. можно сделать квадраты со стороной 9 см и 12 см)
676=100+576=10²+24² (т.е. можно сделать квадраты со стороной 10 см и 24 см)
у = 8,1 * 2 1/4 : 6 3/4
у = 2,7