В решении.
Пошаговое объяснение:
З двох міст, відстань між якими становить 492,8 км, одночасно назустріч один одному виїхали два автобуси. Швидкість одного з них дорівнює 60,7км/год, а швидкість іншого — 62,5 км/год. Через скільки годин автобуси зустрінуться?
Из двух городов, расстояние между которыми составляет 492,8 км, одновременно навстречу друг другу выехали два автобуса. Скорость одного из них равна 60,7 км/ч, а скорость другого - 62,5 км/ч. Через сколько часов автобусы встретятся?
Формула движения: S=v*t
S - расстояние v - скорость t – время
Общее расстояние: 492,8 км;
Общая скорость: 60,7 + 62,5 = 123,2 (км/час);
Общее время t - ?
t = S/v
t = 492,8 : 123,2 = 4 (часа) - через столько часов автобусы встретятся.
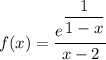1. Рассмотрим точку 11. Тут явно разрыв, так как функция не определена
2. Вычислим односторонние пределы
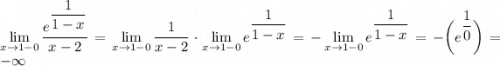
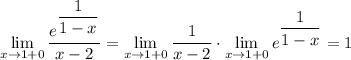
То есть функция сначала ушла в -∞ а затем резко появилась в 1
это разрыв второго рода
2. Рассмотрим точку 21. Тут опять разрыв, смотрим какой
2. Вычислим односторонние пределы
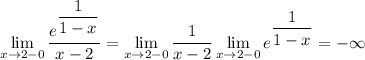
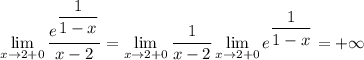
То есть функция сначала уходит в -∞ а потом выходит из +∞
В этой точке тоже разрыв второго рода
19/8+25/8-х=13/8
-х=13/8-19/8-25/8
-х= -31/8
х=31/8=3 7/8