Длина прямоугольника равна 12 см,а ширина-8 см .найди площадьи периметр прямоугольника.

👇

Увидеть ответ

Ответ:

FfffdZb

18.04.2021

Периметр - (12+8)*2=20 см
Площадь 12*8=96 квадр. см

4,4(58 оценок)

Ответ:

KINGAsyaKING

18.04.2021

1)12*8=96-площадь прямоугольника

2) (12+8)*2=40-периметр прямоугольника

4,6(54 оценок)

Открыть все ответы

Ответ:

Kisylyaaa

18.04.2021

1) За 1012 взвешивания Мистер Фокс сможет гарантированно узнать суммарный вес монет.

Он, к примеру, сначала взвесит 1009 "не пересекающихся" пар монет. И узнает их суммарный вес.

Останется еще 3 монеты (по причине того, что 2021 - 1009 · 2 = 3). Первая будет взвешена по очереди со второй и с третьей, а дальше на весах появятся вторая и третья монета.

Результатом таких взвешиваний будут три числа. Если мы их сложим, то получим удвоенный вес первой, второй и третьей монет. Если разделим на два, то получим вес всех трех оставшихся монет.

И прибавим его к весу 1009 пар взвешенных ранее 1009 пар монет. Получим суммарный вес всех монет.

2) Меньше, чем за 1012 взвешиваний, в общем случае суммарный вес монет не удастся узнать.

Почему? Очевидно, что при взвешиваниях каждая монета должна побывать на весах. Поэтому взвешиваний должно быть уже не меньше 1011 (2021 : 2 = 1010 пар монет, и 1 в остатке дает 1011-ое взвешивание).

Несложно понять, что если нам удалось за 1011 взвешиваний узнать суммарный вес монет, то: 1) все монеты побывали на весах; 2) ровно одна монета (обозначим ее буквой М) побывала на весах два раза, во второй раз - с монетой Л, образовавшей в результате остатка при делении на 2 числа 2021.

Суммарный вес всех монет, кроме М нам известен. Следовательно, задача решится, если мы найдем Л. А чтобы найти Л, нужно найти М. Но М как из первого взвешивания, так и из второго найти нельзя.

Так как получается что-то наподобие системы из двух линейных уравнений с тремя неизвестными (X + M = a, M + L = b).

Таким образом, за 1011 (и меньше) взвешиваний узнать суммарный вес всех монет не удастся. А за 1012 - уже получится.

4,4(93 оценок)

Ответ:

class4v2016

18.04.2021

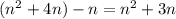Если $n^{2}+4n$ оканчивается числом n, то число $(n^{2}+4n)-n=n^{2}+3n$ оканчивается на четыре нуля, т.е. делится на 10⁴;

Итак, 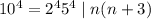$10^{4}=2^{4}5^{4}\;|\;n(n+3)$ ; Теперь степени двойки и пятерки нам нужно раскидать между числами n и n+3; Заметим, что n и n+3 разной четности. Поэтому ровно одно из чисел делится на 2⁴; Поскольку разница чисел равна 3, то оба не могут одновременно делится на 5. То есть ровно одно из чисел делится на 5⁴. Если n делится одновременно на 2⁴ и 5⁴, то оно по крайней мере 10000, но мы рассматриваем четырехзначные числа. Пусть n+3 делится на 2⁴ и 5⁴. Тогда единственное удовлетворяющее условию значение n есть 9997. Запомним.

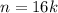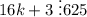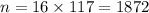Пусть теперь n делится на 2⁴, а n+3 на 5⁴. Тогда n=16k ; Осталось найти наименьшее натуральное такое k, что $16k+3\; \vdots 625$ . Небольшим перебором (по кратным 625) убеждаемся, что 625*3-3 делится на 16, а, значит, наименьшее такое k это 117. Тогда $n=16\times 117=1872$ ;

И последний случай. Пусть n делится на 5⁴, а n+3 на 2⁴. Тогда n нечетно. 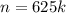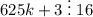n=625k ; $625k+3\;\vdots\;16$ . Наименьшее k тогда 13. 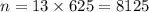$n=13\times625=8125$ . Наименьшее число - 1872