1. B
2. C
3. B
Пошаговое объяснение:
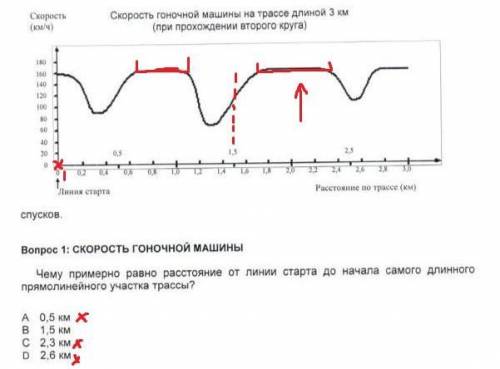
Вопрос 1. Картинка 1.
1. Нужно найти самый длинный прямолинейный участок трассы. (Это будет самая длинная прямая из отмеченных красным на картинке)
2. Опустить прямую от примерного начала этого участка. Увидеть примерную цифру на горизонтальной линии (расстоянии по трассе), куда опустилась наша прямая. Это 1,5 км
Вопрос 2. Картинка 2.
1. Найти "ямки" на графике.
2. Найти самую глубокую "ямку". (соотнести донья ямок с вертикальной линией (скоростью автомобиля)
3. Опустить прямую из самой глубокой "ямки" на горизонтальную линию (расстояние)
4. Получается, точка между 1,2 и 1,4. Значит ответ "Примерно на отметке 1,3 км"
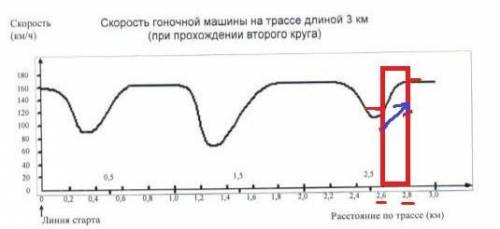
Вопрос 3. Картинка 3.
1. Выделить границы между 2,6 и 2,8 км
2. Отметить точки пересечения графика и наших границ
3. Первая точка ниже второй точки. Следовательно, график возрастает. Значит скорость машины увеличилась.
Пошаговое объяснение: в приложении
Построение раскроев
Пусть даны n типов заготовок с номерами 1,...,n и длинами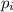
, а исходные стержни имеют длину 
.
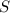В начале поиска полагаем i=1
1. Ищем максимально возможное число заготовок типа i. Оно, очевидно, равно![N=\left[\dfrac{S}{p_i}\right]](/tpl/images/1537/7845/f1eeb.png)
, где [х] - целая часть числа x.
2. Ищем длину незадействованной части стержня. Она, очевидно, равна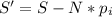
3. Если существует заготовка с номером, большим i, и длиной, меньшей S', и решаем аналогичную задачу для стержня длиной S' и заготовок с номерами i+1,...,n. Иначе пункт 4.
4. Получен вариант раскроя. Записываем число отходов.
5. Если N≥1 и i≠n, уменьшаем N на 1, и решаем аналогичную задачу для стержня длиной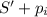
и заготовок с номерами i+1,...,n