Математика: Запишите несколько чисел, каждое из которых кратно и 4, и

Запишите несколько чисел, каждое из которых кратно и 4, и

👇

Увидеть ответ

Ответ:

Vovacool27

11.12.2022

4,8,16,24,28,32
5,10.15,20

4,6(79 оценок)

Открыть все ответы

Ответ:

Вппгш

11.12.2022

1) Водоемы Кубани широко представлены лиманами и плавнями, которые идеальны для рыбной ловли и охоты. Лиманы – это мелководные водоемы, средняя глубина которых составляет от 0,5 до 2,5 метров, сегодня их на территории края насчитывают около 300. Многие степные реки через лиманы связаны с морем.
2)Реки Черноморского побережья резко отличаются от рек Азово-Кубанской низменности, ближе они по облику к горным рекам бассейна Кубани, но формируются в несколько иных природных условиях.Реки степей Кубани и плавневой зоны Азова заметно отличаются от левых притоков р. Кубань и рек Черноморского побережья: водным режимом, строением долин, и большинство их названий имеет тюркское происхождение. Междуречья здесь плоские с довольно малой расчлененностью. Речные долины, как правило, широкие с пологими берегами. Незначительные уклоны рек спокойному течению. Почти все их долины параллельно вытянуты с юго-востока на северо-запад. Исключение составляют две речки: Албаши и Ясени, долины которых вытянуты почти с северо-востока на юго-запад. Притоки рек называют балками, в отличие от притоков левобережных рек Кубани и Черноморского бассейна, которые зачастую называют щелями.
3)Черный тополь, тростник южный, цикорий,
4)еографическое положение и природные условия Азовского моря предопределяют развитие хозяйственной деятельности на нем. До 50-х годов это был один из основных рыбопромысловых водоемов страны, поставлявший ценные виды рыбы и рыбной продукции пищевого направления. В последние 25 лет его роль в рыболовстве страны снизилась, уловы сократились. В настоящее время на Азовском море усилились рыбоводные мероприятия, что открыло пути восстановлению его рыбных богатств, главным образом осетровых.Геологической разведкой установлены запасы нефти под морским дном. В связи с этим проводится поисковое бурение на нефть, которая в перспективе может быть использована для промышленной разработки.С давних времен Азовское море стало транспортной артерией страны. В настоящее время эта отрасль хозяйства получила широкое развитие. В море осуществляются не только каботажные перевозки (они преобладают), но и проходят международные судоходные пути. Море связывает внутренние районы Советского Союза с зарубежными странами. Благоприятные климатические условия позволяют использовать Азовское побережье в рекреационных целях. Сотни здравниц раскинулись на берегах Азовского моря.Несмотря на довольно хорошую изученность Азовского моря, в настоящее время существует еще немало проблем его исследования. Главная из них — прогноз будущего облика природы моря в условиях дальнейшего снижения речного стока и на этой основе разработка эффективных мероприятий по сохранению оптимального режима Азовского моря. Определяющую роль в природных процессах в море играет соленость, поэтому основное звено комплексной проблемы — изучение режима солености и выбор путей предотвращения прогрессирующего осолонения Азовского моря, в частности всесторонняя оценка эффективности воздействия проектируемого Керченского гидроузла на весь комплекс природных условий Азовского моря. В качестве одного из путей изучения Азовского моря намечается и осуществляется разработка экономико-экологической модели этого водоема, которая связывает все элементы природы и хозяйства моря и тем самым решению комплексной проблемы этого водоема

4,4(39 оценок)

Ответ:

susannamuratov1

11.12.2022

А)

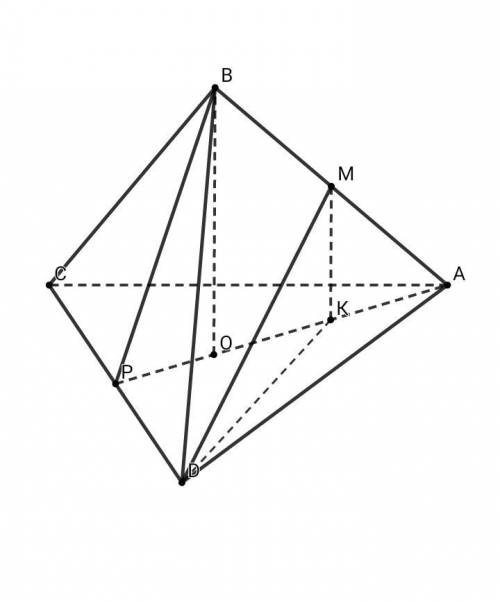
DABC - правильный тетраэдр ⇒ все рёбра данного тетраэдра равны, и грани представляют собой равные правильные треугольник. Чтобы было удобнее, расположим тетраэдр на грань ACD, что никак не изменяет его. Вершина тетраэдра проецирется в центр основания(ΔACD - правильный), то есть в точку пересечения биссектрис, медиан и высот, и поэтому падает на медиану АР, BO⊥AP ⇒ (АВР)⊥(ACD), а значит, ортогональная проекция точки на плоскость ACD лежит на медиане AP, MK⊥AP, ч.т.д.

Б)

Не зря ж доказывали, что проекция точки М падает на AP, это пригодиться и под пунктом Б) ; MK⊥AP ⇒ MK⊥(ACD), MK⊥DK, а значит, ∠MDK - искомый угол между прямой DM и плоскостью ACD. Пусть все рёбра тетраэдра равны 1, тогда в правильном ΔABD: DM - медиана, высота, биссектриса и рассчитывается по формуле DM = a√(3)/2 = √(3)/2. Медианы треугольника пересекаются точкой пересечения в отношении 2 : 1, считая от вершины: AO = 2•OP ; BO⊥AP, MK⊥AP ⇒ BO||MK и ВМ = АМ, значит, АК = КО = ОР ; АР - высота правильного ΔACD ⇒ AP = √(3)/2 , AK = KO = OP = AP/3 = √(3)/6 ; PK = √(3)/3 ; CP = PD = CD/2 = 1/2 ⇒ по т.Пифагора в прям-ом ΔKPD: KD² = PK² + PD² = (√(3)/3)² + (1/2)² = (1/3) + (1/4) = 7/12 ⇒ KD = √(7/12)

В прям-ом ΔMDK: cos∠MDK = KD/DM = √(7/12) : (√(3)/2) = 2√7/√36 = √(7)/3 ⇒ ∠MDK = arccos(√(7)/3)

ответ: б) arccos(√(7)/3)