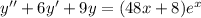
Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.
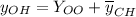
Решим однородное дифференциальное уравнение, соответствующее данному неоднородному:
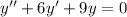
Составим и решим характеристическое уравнение:
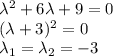
Запишем общее решение однородного уравнения:
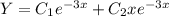
Частное решение будем искать в виде:
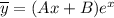
Найдем первую и вторую производную:
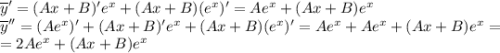
Подставим значения функции и первых двух производных в исходное уравнение:
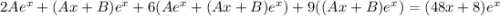
Сократим на 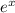 :
:
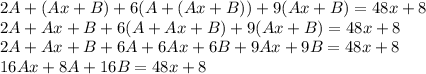
Так как левая и правая часть равны, то коэффициенты при х и свободные члены также равны. Получаем систему:
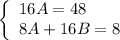
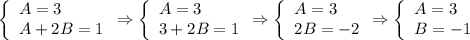
Тогда частное решение имеет вид:
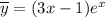
Общее решение заданного уравнения:
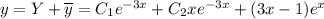
ответ: 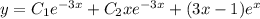
Задание 1
5298,5299,5300,5301,5302,5303,5304,5305.5306,5307
Задание 2
15 единиц 4 класса - 15 000 000 000
30 единиц 3 класса - 30 000 000
567 единиц 2 класса - 567 000
306 единиц 1 класса - 306
Задание 3
64000÷1000=64
7800×10=78000
3000+400+50+9=3459
400376-400000-70=306
Задание 4
(625-189)+(414-325)- 129=218
625-189=436
414-325=89
436-89-129=218
(100•9:30)+120:2+140=
100•9=900
900:30=30
120:2=60
30+60+140=230
Задание 5
1)63/7=9( деталей /ч)-токарь
2)30/6=5(деталей/ч)-ученик
3)9-5=4(д./ч)-больше
Задание 6
108÷а=9
а=108÷9
а=12
b:3=11
b=11×3
b=33
14×с=42
с=42:14
с=3
Задание 7
1)7 - 687:4= 171(ост 7)
2)865:3=228 (ост 3)