Веревку разрезали на 3 части. в первой части- 0,4 длины всей веревки , во второй 0,5 её длины , ав третьей 12 м .чему ровная длина всей веревки?

👇

Ответ:

ramil161

23.04.2020

Вся верёвка х
первая часть 0,4х
вторая часть 0,5х
третья часть 12 м
х-0,4х-0,5х=12
0,1х=12
х=12:0,1
х=120 м вся верёвка составляет третья часть
12:0,1=120 м вся верёвка

4,6(82 оценок)

Открыть все ответы

Ответ:

redvellk7

23.04.2020

Знаки препинания.
Знаки препинания нам писать грамотно,доносить свою мысль верно(.можешь взять в других источниках или в этих ,откуда точнее кто изобрёл первые знаки препинания,.Далее можешь написать как ранние знаки препинания (пунктуация))Предложения в тексте отделяются друг от друга различными знаками препинания: точкой, многоточием, вопросительным и восклицательным знаками. Эти знаки препинания не только организуют письменный текст для облегчения его восприятия читателем, но и передают часть заключенной в тексте информации.
Так, поставленная в конце предложения точка сигнализирует о том, что предложение содержит повествование или побуждение .
Многоточие передает недосказанность, недоговоренность.
Вопросительный знак ставится для выражения вопроса или сомнения , а восклицательный – для передачи эмоционального состояния, восклицания, удивления .
Таким образом, все вышеперечисленные знаки препинания выбрать правильную интонацию предложения, а также понять смысл написанного.
Запятая – это один важных знаков препинания, без которого действительно обойтись невозможно.
Запятые в предложениях выполняют разные функции. Во-первых, запятая может употребляться в разделительной функции.
Во-вторых, очень важна выделительная функция запятых.
В заключение хотелось бы сказать, что запятая – это многофункциональный знак препинания, от правильной расстановки которого зависит понимание смысла написанного.
В сложных предложениях могут употребляться запятая, точка с запятой, тире, двоеточие. Роль этих знаков препинания огромна, потому что они выполняют разные функции: разделительную, выделительную, смысловую, интонационную.
Во-первых, в сложных синтаксических конструкциях знаки препинания нередко служат для разделения частей.
Во-вторых, в сложноподчинённых предложениях запятые могут выполнять выделительную функцию. Двоеточие и тире в сложных предложениях могут выполнять смыслоразличительную функцию.

4,7(42 оценок)

Ответ:

danyok132006

23.04.2020

МС=МД=МА=МВ=√29,5см

Пошаговое объяснение:

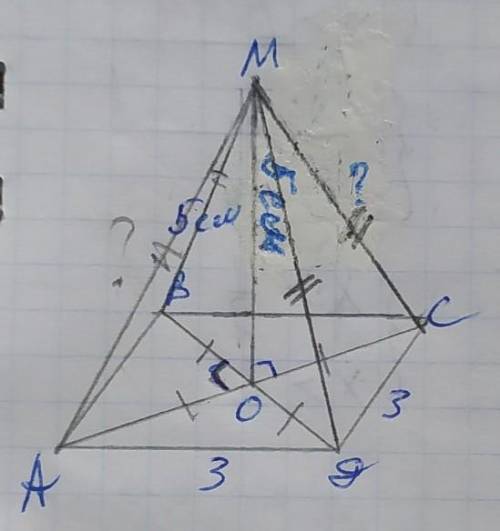
Обозначим вершины квадрата А В С Д с диагоналями АС и ВД. Диагонали квадрата пересекаются под прямым углом и точкой пересечения делятся пополам, поэтому АО=СО=ВО=ДО. Одна диагональ делит квадрат на 2 равных прямоугольных треугольника, в которых диагональ является гипотенузой, а стороны квадрата катетами. Найдём диагональ АС по теореме Пифагора:

АС²=АД²+СД²=3²+3²=9+9=18;

АС=√18=3√2см, тогда

АО=СО=3√2÷2=1,5√2см.

Так как перпендикуляр МО проведён в точку пересечения диагоналей, то он равноудалён от всех вершин квадрата. Рассмотрим ∆МСО: перпендикуляр МО образует с СО прямой угол, значит этот треугольник прямоугольный, в котором МО и СО –катеты, а наклонная МС – гипотенуза.

Найдём её по теореме Пифагора:

МС²=МО²+СО²=5²+(1,5√2)²=25+2,25×2=25+4,5=29,5

МС=√29,5см

МС=МД=МА=МВ=√29,5см