Неравенство ax² + bx + c < 0 не будет иметь решений, если парабола
y = ax² + bx + c будет расположена над осью Ох или будет касаться оси.
Для этого коэффициент а должен быть положительным, а уравнение ax² + bx + c = 0 не должно иметь корней или иметь один корень, т.е. дискриминант должен быть меньше либо равен нулю:
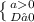
(p - 1) x² + (p - 2) x + 3p - 1 < 0
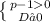
D = (p - 2)² - 4(p - 1)(3p - 1) = p² - 4p + 4 - 12p² + 16p - 4 = - 11p² + 12p
- 11p² + 12p ≤ 0
p(11p - 12) ≥ 0 (см. рис. 1)
p ∈ (- ∞ ; 0] ∪ [12/11 ; + ∞)
p > 1
(см. рис. 2)
p ∈[12/11 ; + ∞)
1) Сколько было булав и колец, если бы их было поровну?
27 - 13 = 14 (пр.)
Мы знаем, что если булав и колец было поровну, то было всего 14 предметов.
Если вы уже изучили действе деление, то легко можно вычислить, сколько было колец и булав по отдельности:
2) 14 : 2 = 7 (пр.), то есть было 7 колец и 7 булав
Если вы не изучали действие деление, то решить еще проще: мы знаем состав двузначных чисел и знаем, что
14 - это 7 и 7, то есть было 7 колец и 7 булав
Рассуждаем дальше:
По условию задачи булав было больше на 13 штук, значит, сложение, знак плюс:
3) Сколько было булав?
7 + 13 = 20 (б.)
ответ: было 7 колец и 20 булав.
Проверка:
20 + 7 = 27 (пр.) - как в условии задачи
Запись задачи без пояснений:
1) Сколько было булав и колец, если бы их было поровну?
27 - 13 = 14 (пр.)
2) Сколько было колец?
14 : 2 = 7 (пр.)
или
14 - это 7 и 7
3) Сколько было булав?
7 + 13 = 20 (б.)
ответ: было 7 колец и 20 булав.
y=ln(x^4*arctg(2x)-((5^x)/cos^7(3x))
y ' =(1/(x^4*arctg(2x)-((5^x)/cos^7(3x))) * (4x^3*arctg(2x)+x^4*(1/(1+4x^2)*2-((5^x)*ln(5)*cos^7(3x)-(5^x)*7*cos^6(3x)*(-sin(3x)*3)/cos^14(3x))=
=((4x^3*arctg(2x)+x^4*(1/(1+4x^2)*2-((5^x)*ln(5)*cos^7(3x)+21*(5^x)*cos^6(3x)*sin(3x))/cos^14(3x)) : (x^4*arctg(2x)-((5^x)/cos^7(3x))
При расчете использованы формулы
(ln(x) ' =1/x
(uv) ' = u 'v+v'u
(u/v) ' = (u'v-v'u)/v^2
(arctg(x)) ' = 1/(1+x^2)
(sin(x)) ' = -cos(x)
(a^x) ' =a^x * ln(a)