1) Дана функция y= -x^3-3x^2+4.
Её производная равна y' = -3x² - 6x = -3x(x + 2).
Приравняем её нулю: -3x(x + 2) = 0. Находим 2 критические точки:
х = 0 и х = -2.
Определяем их свойства по изменению знака производной.
х = -3 -2 -1 0 1
y' = -9 0 3 0 -9 .
В точке х = -2 минимум функции, у = 0.
В точке х = 0 максимум, у = 4.
На промежутках (-∞; -2) и (0; +∞) функция убывает
на промежутке (-2; 0) возрастает.
Вторая производная равна y'' = -6x - 6 = -6(x + 1).
Отсюда определяем точку перегиба х = -1.
х = -2 -1 0
y'' = 6 0 -6.
График выпуклый: (-1; +∞), вогнутый (-∞; -1).
Пересечение с осями решается алгебраически:
- с осью Оу при х = 0 у = 4.
- с осью Ох при у = 0 надо решить кубическое уравнение
-x^3-3x^2+4 = 0. Один корень виден: х = 1.
Делим -x³ - 3x² + 4 | х - 1
-x³ + x² -x² - 4x - 4
-4x² + 4
-4x² + 4x
-4x + 4
-4x + 4.
Результат -(x² + 4x + 4) = -(х + 2)².
Получили 2 точки пересечения: х = 1 и х = -2.
График приведен в приложении.
2) Возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже. Эти случаи легко различаются с дискриминанта
Δ = -4b³d + b²c² - 4ac³ + 18abcd - 27a²d².
Итак, возможны только три случая:
Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
Если Δ = 0, тогда хотя бы два корня совпадают.
Рассмотрим уравнение -x^3-3x^2+4=0.
Его коэффициенты a b c d
-1 -3 0 4
Определяем дискриминант:
-4b^3*d b^2*c^2 -4a*c^3 18abcd -27*a^2*d^2 Дискрим
инант
432 0 0 0 -432 0.
Как видим, при а = 0 уравнение имеет 2 корня.
Это видно и по графику.
После двух дней продажи в магазине осталась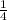 
часть от всего картофеля.
Туристы запасли 40 кг провизии. На третий день осталось 19,6 кг еды.
Задание №3:Пятиклассники собрали всего 144 кг или 1 центнер 44 кг грибов и ягод.
Пошаговое объяснение:
Задание №1:Узнаем массу картофеля, завезённого в магазин:
1) 240 : 4 = * 10 = 600 ( кг ) - масса картофеля, завезённого в магазин.
Узнаем массу картофеля, оставшегося после первого дня продажи:
2) 600 - 240 = 360 ( кг ) - масса картофеля, оставшегося после первого дня продажи.
Узнаем массу картофеля, проданного во второй день:
3) 360 : 12 * 7 = 210 ( кг ) - масса картофеля, проданного во второй день.
Узнаем массу картофеля, оставшегося после двух дней продажи:
4) 360 - 210 = 150 ( кг ) - масса картофеля, оставшегося после двух дней продажи.
Узнаем какую часть от всего картофеля составляет оставшийся после двух дней продажи картофель:
5) 150 : 600 = 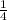- часть от всего картофеля.
Узнаем какую часть от всех запасов съели туристы во второй день:
1) 0,36 : 12 * 5 = 0,15 - часть от всех запасов съели туристы во второй день.
Узнаем размер запасов:
2) 6 : 15 * 100 = 40 ( кг ) - размер запасов.
Узнаем размер запасов, съеденных туристами в первый день:
3) 40 : 100 * 36 = 14,4 ( кг ) - размер запасов, съеденных туристами в первый день.
Узнаем размер запасов, съеденных туристами за второй день:
4) 14,4 : 12 * 5 = 6 ( кг ) - размер запасов, съеденных туристами за второй день.
Узнаем размер запасов, съеденных туристами за первый и второй дни:
5) 14,4 + 6 = 20,4 ( кг ) - масса всех запасов, съеденных туристами за первый и второй дни.
Узнаем размер запасов, оставшихся на третий день:
6) 40 - 20,4 = 19,6 ( кг ) - размер запасов, оставшихся на третий день.
Задание №3:Узнаем массу всех грибов:
1) 64 : 4 * 7 = 112 ( кг ) - масса всех грибов.
Узнаем массу всех грибов и ягод:
2) 112 : 7 * 9 = 144 ( кг ) - масса всех грибов и ягод.
Перевод:
144 кг = 1 ц 44 кг
УДАЧИ! ОБРАЩАЙТЕСЬ!
5*6=30 - это скорость мотоцикла.
Получается, что скорость теплохода и мотоцикла равны.