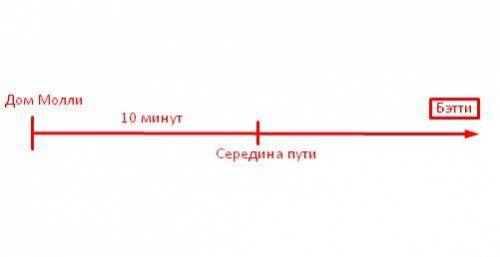
Улитка Молли поползла на день рождение черепахи Бэтти, но, когда она проползла половину пути до дома Бэтти, Молли вспомнила, что забыла подарок дома. Она развернулась и с той же скоростью поползла обратно. Взяла подарок и с той же скоростью поползла к Бэтти. К Бэтти она приползла на 20 минут позже, чем планировала. Сколько минут у Молли занимает дорога от её дома до дома Бэтти?
Весь путь Молли преодолевала с одинаковой скоростью (по условию)
Тогда, расстояние "Дом - середина пути" и "середина пути - дом" одно и тоже и равняется расстоянию "середина пути - Бэтти". Таким образом можно утверждать, что Молли расстояния "Дом - Бэтти" тем самым удвоив время пути до нее.
Следовательно - время опоздания равняется времени пути от дома до Бэтти.
ответ: 20 минут
Альфа I, Дельта II, Гамма III, Бетта IV
Пошаговое объяснение:
Альфа I и Бетта II --> первое утверждение
Альфа II и Гамма III --> второе утверждение
Дельта II и Гамма IV --> третье утверждение
Если Альфа I, то Бетта НЕ II --> следует из первого утверждения
Если Альфа I, то Альфа НЕ II и Гамма III --> следует из первого и второго утверждения
Если Гамма III, то Гамма НЕ IV и Дельта II --> следует из второго и третьего утверждения
Значит Бетта IV, потому как остальные места заняты
Альфа I Верно и Бетта II Неверно --> первое утверждение
Альфа II Неверно и Гамма III Верно --> второе утверждение
Дельта II Верно и Гамма IV Неверно --> третье утверждение
Первый ряд можно сравнить с заведомо сходящимся рядом:
(2n+2)/(3n^3 + 3) меньше 4/3n^2. Значит ряд сходится.
Что касается второго ряда, то если бы n прин [2; беск], то ряд сходится абсолютно по теореме Лейбница. Но в условии n - от 1 до бескон. А при n = 1 a1 = бесконечности...Поэтому ряд расходится. Может в условии все-таки n стартует от 2???