В России проживает около 190 национальностей. Для примера возьмем татар и опишем традиции их народа. Татары каждую весну празднуют Сабантуй плуга. Праздник символизирует конец посева. На празднике проводятся разные соревнования и состязания. Бег, борьба, скачки на лошадях – за этим наблюдают много людей. Обязательным угощением в этот день будет боткасы. А еще на праздник приносят много крашеных яиц для детей.
Также они празднуют религиозные праздники. Рамадан, в котором постятся все верующие мусульмане. Днем запрещается работать, есть и пить. В это время нужно размышлять над прочитанным в Коране и молиться.
Празднуют татары Корбан-Байрам. Праздник жертвоприношения отмечается по Корану. Согласно Корану, Аллах заменил сына Авраама ягненком. Праздник символизирует примирение и милосердие. В этот день делают угощения для всех.
Одним из народных праздников татаров является Боз карау. Боз карау означает «смотреть на лед». Раньше многие татарские села находились возле рек. На берег выходили жители села и смотрели на ход льда. Пели песни в этот день и играли в разные игры.
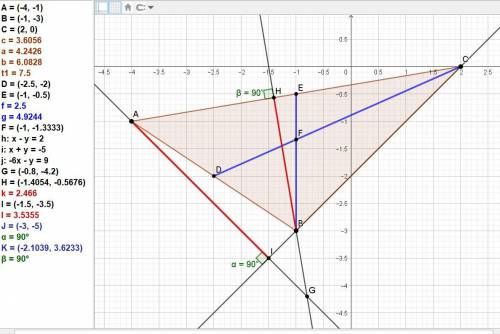
Даны координаты вершин A(-4;-1) B(-1;-3) C(2;0).
Найти точки пересечения медиан и высот треугольника АВС.
1) Точка F пересечения медиан треугольника имеет следующие координаты:
x(F) = (x1+x2+x3)/3, y(F) = (y1+y2+y3)/3,
где A(x1,y1), B(x2,y2) и C(x3,y3) − вершины треугольника ABC.
Подставим координаты точек и получаем ответ.
х(F) = (-4+(-1)+2)/3 = -1,
у(F) = (-1+(-3)+0)/3 = -4/3.
ответ: точка пересечения медиан F(-1; (-4/3)).
2) Находим уравнения сторон, для чего определяем векторы АС и ВС.
Вектор АС = ((2-(-4)); (0-(-1)) = (6; 1).
Уравнение АС: (x + 4)/6 = (y + 1)/1 каноническое.
x – 6y – 2 = 0 общее.
Вектор ВС = ((2-(-1)); (0-(-3)) = (3; 3).
Уравнение ВС: (x + 1)/ 6 = (y + 3)3 каноническое.
3x – 6y – 15 = 0 общее или, сократив на 3
x – 2y –5 = 0.
Теперь находим уравнения высот к этим сторонам.
Уравнение высоты BH.
Она перпендикулярна стороне AС.
Вектор AС найден и равен (6; 1).
Для прямой BH он будет нормальным вектором.
Составляем уравнение прямой по точке В(-1; -3) и нормальному вектору (6; 1).
Уравнение BH: 6*(x + 1) + 1*(y + 3) = 0,
6x + 6 + y + 3= 0,
6x + y + 9 = 0.
Уравнение высоты AI.
Она перпендикулярна стороне BС.
Вектор BС найден и равен (3; 3).
Для прямой AI он будет нормальным вектором.
Составляем уравнение прямой по точке A(-4; -1) и нормальному вектору (3; 3).
Уравнение AI: 3*(x + 4) + 3*(y + 1) = 0,
3x + 12 + 3y + 3= 0,
3x + 3y + 15 = 0 или, сократив на 3:
x + y + 5 = 0.
Координаты точки G пересечения высот найдём, решив систему:
{6x + y + 9 = 0
{ x + y + 5 = 0 вычтем из первого уравнения второе.
5x + 4 = 0, отсюда х = -4/5 = -0,8.
у = -х – 5 = -(-0,8) – 5 = -4,2.
ответ: точка пересечения высот G(-0,8; -4,2).
1/8-x=(3x+1/8)·4
1/8 -x= 12x+1/2
13x=-3/8
x=-13·8/3=-104/3