Кількість можливих варіантів розміщень з n = 4 по
k = 3 без повторень можна визначити за формулою:
An->k = n!/(n−k)!
A4->3 = 4!/(4-3)! = 4! = 4×3×2 = 24
Отже, таких чисел 24.
1) 1 на першому місці:
123, 132, 124, 142, 134, 143.
2) 2 на першому місці:
213, 214, 234, 231, 243, 241.
3) 3 на першому місці:
312, 314, 321, 324, 341, 342.
4) 4 на першому місці:
412, 413, 421, 423, 431, 432.
Відповідь: 24 числа:
123, 132, 124, 142, 134, 143,
213, 214, 234, 231, 243, 241,
312, 314, 321, 324, 341, 342,
412, 413, 421, 423, 431, 432.
Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда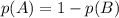 
Вероятность не угадать число на одном кубике равна 
(среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна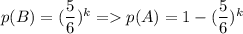 
- это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна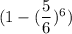 
. При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 
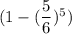. При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна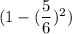 
Тогда искомая вероятность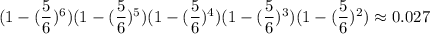 
б) 7500 кг = 7,5 тонн