Составить сообщение об одном из народов россии и мира или о любой стране

👇

Ответ:

DDddd532222

04.05.2020

Эскимосы— народ, составляющий коренное население территории от Гренландии и Нунавута (Канада) до Аляски (США) и восточного края Чукотки (Россия). Численность — около 170 тыс. человек. Бытовая их культура необычайно при к Арктике. Они изобрели поворачиваемый гарпун, чтобы охотиться на морского зверя, каяк, снежный дом иглу, особую глухую одежду из меха и шкур. В XIX веке эскимосы не имели родовой и развитой племенной организации. В результате контактов с пришлым населением в жизни зарубежных эскимосов произошли большие изменения. Значительная их часть перешла от морского промысла к охоте на песцов, а в Гренландии — к товарному рыболовству. Повсюду остатки традиционной культуры эскимосов быстро исчезают.В России эскимосы — малочисленная этническая группа (по данным переписи 2002 г. 1750 человек), живущая смешанно или в близком соседстве с чукчами в ряде населенных пунктов восточного побережья Чукотки и на острове Врангеля. Их традиционные занятия — морской зверобойный промысел, оленеводство, охота. Эскимосы верят в духов, живущих в различных явлениях природы, видят связь человека с окружающим его миром предметов и живых существ. Существуют также представления о злых духах. Бубен для эскимосов — священный предмет. Традиционное приветствие, называемое «эскимосским поцелуем», стало всемирно известным жестом.Рацион эскимосов в основном состоит из мяса и рыбы, преимущественно сырых, а также небольшого количества трав, ягод и водорослей. Эскимосы Канады используют собственную письменность на основе канадского слогового письма.

4,4(15 оценок)

Открыть все ответы

Ответ:

vvbedash

04.05.2020

3+2+4=9 - это все части

90:9=10 - это на одну часть

10×3=30 (см) - это на 1ю часть

10×2=20 (см) - это на 2ю часть

10×4=40 (см) - это на 3ю часть

ответ: 30,20,40

Треугольники МNК и ANB подобны, т.к. прямая, паралельная одной из сторон треугольника и пересекающая две другие его стороны, отсекает треугольник, подобный данному. Отношение медиан в подобных треугольниках равно отношению сходственных сторон. Иедианы , точкой пересечения делятся 2: 1 считая от вершины. Тогда АВ:МК=МО:NP, где Р-это точка пересечения медианы NP со стороной МК Пусть МК=х х:12=3:2 х=18 см.

По теореме Пифагора АВ=корень из ВС^2+АС^2=корень из 100+100=200см.-длина гипотенузы. Т к катет АС(10см) в 2раза меньше гипотенузы АВ(200см), то угол В=300градусов., может быть, но это не точно, в общем за теоремой Пифагора решаеться задача.

4,6(71 оценок)

Ответ:

Кея1563

04.05.2020

Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.

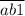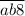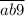Значит, эти числа либо от $\overline{ab1}$ до $\overline{ab8}$ , либо от $\overline{ab2}$ до $\overline{ab9}$ .

Значит, в любом случае среди этих чисел есть следующие:

$\overline{ab2}$ , делящееся на 2

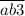$\overline{ab3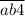}$ , делящееся на 3

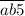$\overline{ab4}$ , делящееся на 4

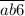$\overline{ab5}$ , делящееся на 5

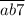$\overline{ab6}$ , делящееся на 6

$\overline{ab7}$ , делящееся на 7

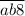$\overline{ab8}$ , делящееся на 8

Рассмотрим утверждение "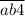 $\overline{ab4}$ делится на 4". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит 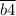$\overline{b4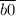}$ делится на 4, 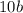$\overline{b0}$ делится на 4, 10b делится на 4, 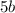делится на 2, значит 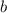- четное.

Рассмотрим утверждение "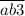 $\overline{ab3}$ делится на 3". Число делится на 3, если сумма цифр числа делится на 3. Значит, 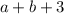a+b+3 делится на 3, 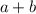a+b делится на 3. Выпишем пары цифр, где 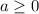$a\geq 0$ , а 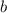- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).

Рассмотрим утверждение "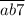 $\overline{ab7}$ делится на 7". Если 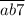$\overline{ab7}$ делится на 7, то 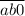$\overline{ab0}$ делится на 7, 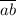$\overline{ab}$ делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.

Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.

Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.

ответ: 13

4,8(26 оценок)

Это интересно:

Образование-и-коммуникации

01.09.2020

Как нарисовать банан: подробная инструкция для начинающих...

Стиль-и-уход-за-собой

07.05.2020

Правильный выбор парика: все, что вам нужно знать...

Компьютеры-и-электроника

04.07.2022