Так как три стороны искомого четырёхугольника – это стороны исходного треугольника, то вписанная в четырёхугольник окружность является и вписанной в треугольник.
То есть такая окружность – единственная и её радиус определяется размерами треугольника.
Радиус окружности r = S/p.
Площадь треугольника определяем по формуле Герона.
Полупериметр р = (30+30+36)/2 = 96/2 = 48.
S = √(p(p-a)(p-b)(p-c)) = √(48*18*18*12) = √186624 = 432 кв.ед.
Получаем r = 432/48 = 9.
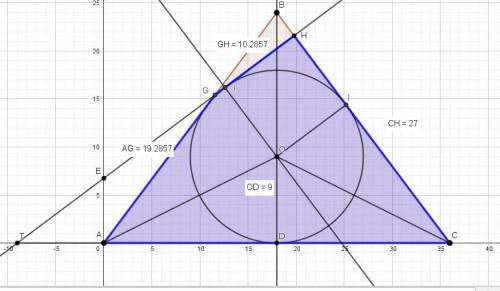
Заданная прямая, образующая четырёхугольник, это касательная к окружности и перпендикулярная боковой стороне.
Длина отрезка СН = 18 + 9 = 27.
Находим тригонометрические функции угла С.
Определяем высоту BD = 2S/AC = 2*432/36 = 24.
sin C = 24/30 = 4/5, cos C = 18/30 = 3/5, tg C = 24/18 = 4/3.
Находим координаты точки Н.
x(H) = 36 – 27*cos C = 36 – (27*3/5) = 99/5 = 19,8.
y(H) = 27*sin C = 27*(4/5) = 108/5 = 21,6.
Координаты точки G находим как точку пересечения прямых AB и GH.
Уравнение АВ: у = (4/3)х.
Уравнение ВС: у = (-4/3)х + (36*4/3) = (-4/3)х + 48.
Угловой коэффициент к перпендикулярной прямой GH равен: к = -1/(-4/3) = 3/4.
Уравнение GH: y = (3/4)x + b. Для определения параметра b подставим координаты точки Н: 21,6 = (3/4)*19,8 + b, отсюда b = 6,75.
Уравнение GH: y = (3/4)x + 6,75.
Приравниваем (4/3)x = (3/4)x + 6,75.
Получаем x(G) = 81/7, y(G) = 108/7.
Имея координаты четырёх точек находим площадь искомого четырёхугльника.
Примем условные координаты точек.
Площадь треугольника ABC
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 27,77143
Площадь треугольника ACD 388,8
Площадь четырёхугольника АBCD S(ABCD)= 416,5714.
S(AGHC)= 416,5714.
H1 = (из первой урны вытащили белый шар, из второй вытащили черный шар; тогда в третьей урне будет 5 белых и 9 черных),
H2 = (из первой урны вытащили белый шар, из второй вытащили белый шар; тогда в третьей урне будет 4 белых и 10 черных),
H3 = (из первой урны вытащили черный шар, из второй вытащили черный шар; тогда в третьей урне будет 6 белых и 8 черных),
H4 = (из первой урны вытащили черный шар, из второй вытащили белый шар; тогда в третьей урне будет 5 белых и 9 черных).
Найдем вероятности гипотез по классическому определению вероятности:
P(H1) = 1/(1+9) * 1/(1+5) = 1/60
P(H2) = 1/(1+9) * 5/(1+5) = 5/60
P(H3) = 9/(1+9) * 1/(1+5) = 9/60
P(H4) = 9/(1+9) * 5/(1+5) = 45/60
Введем событие A = (из третьей урны вытащили белый шар).
Подсчитаем априорные вероятности:
P(A|H1) = P(A|H4) = 5/(5+9)
P(A|H2) = 4/(4+10)
P(A|H3) = 6/(6+8)
Вероятность события A найдем по формуле полной вероятности:
P(A)=P(A|H1)P(H1)+P(A|H2)P(H2)+P(A|H3)P(H3)+P(A|H4)P(H4)
P(A)=5/14*1/60+4/14*5/60+6/14*9/60+5/14*45/60=5/840+20/840+54/840+225/840=304/840=0.3619
ответ: 0.3619