Гипотезы:
A₁ - взятая лампа с первого завода,
A₂ - взятая лампа со второго завода,
A₃ - взятая лампа с третьего завода.
P(A₁) = 5t/(5t+3t+2t) = 5/10 = 0,5
P(A₂) = 3t/(5t+3t+2t) = 3/10 = 0,3
P(A₃) = 2t/(5t+3t+2t) = 2/10 = 0,2
Событие B - взятая лампа исправна.
P(B) = P(B*(A₁UA₂UA₃)) = P( BA₁ U BA₂ U BA₃) =
= P(BA₁) + P(BA₂) + P(BA₃) = P(B|A₁)*P(A₁) + P(B|A₂)*P(A₂) + P(B|A₃)*P(A₃),
По условию:
P(B|A₁) = 0,8
P(B|A₂) = 0,9
P(B|A₃) = 0,7.
P(B) = 0,8*0,5 + 0,9*0,3 + 0,7*0,2 = 0,4 + 0,27 + 0,14 = 0,4 + 0,41 = 0,81
P(BA₂) = P(B|A₂)*P(A₂)
P(BA₂) = P(A₂B) = P(A₂|B)*P(B),
P(A₂|B)*P(B) = P(B|A₂)*P(A₂),
По условию требуется найти P(A₂|B). Из последнего равенства имеем:
P(A₂|B) = P(B|A₂)*P(A₂)/P(B) = 0,9*0,3/0,81 = 0,27/0,81 = 27/81 = 3/9 = 1/3.
ответ. 1/3.
Пошаговое объяснение:
сначала найдем координаты векторов АВ и АС
AB = {Bx - Ax; By - Ay; Bz - Az} = {-1 - (-1); -1 - (-2); 0 - (-1)} = {0; 1; 1}
AC = {Cx - Ax; Cy - Ay; Cz - Az} = {-1 - (-1); -1 - (-2); -1 - (-1)} = {0; 1; 0}
теперь скалярное произведение
AB * AC = ABx * ACx + ABy * ACy + ABz * ACz = 0 * 0 + 1 *1 + (-1) * 0 = 0+1+0 = 1
теперь длины векторов
|AB| = √(ABx)² + ABy² + ABz²) = √(0² + 1² + (-1)²) = √(0 + 1 + 1) = √2
|AC| = √(ACx² + ACy² + ACz²) = √(0² + 1² + 0²) = √(0 + 1 + 0) = √1 = 1
теперь cos A
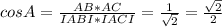
∠A = 45°
а если по 15 то останутся неположенные печенья или в 1 коробке будет меньше печений