1) 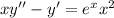
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на 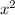 , получаем
, получаем
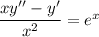
В левой части уравнения это ни что иное как формула производной частного, то есть :
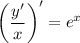
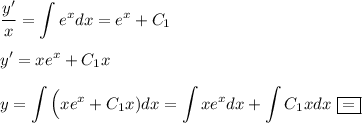
Подсчитаем отдельный интеграл 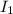 по частям.
по частям.
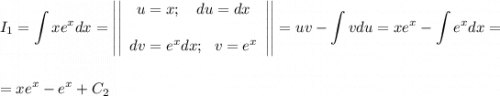
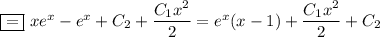
2) 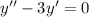
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена 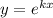 , перейдём к характеристическому уравнению:
, перейдём к характеристическому уравнению: 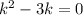 ,
, 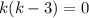 корни которого
корни которого 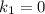 и
и 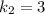 . Тогда общее решение диф. уравнения:
. Тогда общее решение диф. уравнения: 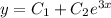 и его первая производная
и его первая производная 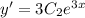 .
.
Осталось найти константы C₁ и C₂ , подставляя начальные условия.
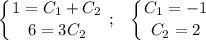
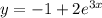 — частное решение.
— частное решение.
это слишком лекго