Необходимо сложить первые 16 последовательных натуральных чисел
Пошаговое объяснение:
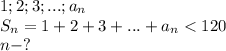
Данная последовательность представляет арифметическую прогрессию, первый член которой равен 1, последний a(n) и разность прогрессии 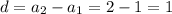
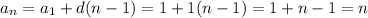
Сумма данной арифметической прогрессии
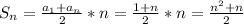
По условию, сумма данной прогрессии должна быть больше 120. Составим и решим неравенство:
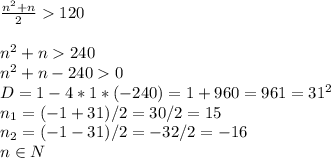
(n-15)(n+16)>0
+ - +
________ -16______0______15______
| //////////////////
n>15
По условию, число n должно быть минимальным.
Следовательно, n=16
log(0,3) (12 - 6x) <= log (0,3) (x^2 -6x + 8) + log (0,3) (x+3)
log(a) b ОДЗ a>0 b>0 a≠1
итак ищем ОДЗ тело логарифма больше 0
1. 12 - 6x > 0 x < 2
2. x^2 - 6x + 8 > 0
D = 36 - 32 = 4
x12=(6+-2)/2=4 2
(х - 2)(х - 4) > 0
x∈ (-∞ 2) U (4 +∞)
3. x + 3 > 0 x > -3
ОДЗ x∈(-3 2)
так как основание логарифма меньше 1, поэтому знак меняется на >= c <= (противоположный)
12 - 6x ≥ (x^2 - 6x + 8)(x + 3)
6(2 - x) ≥ (x - 2)(x - 4)(x + 3)
6(x - 2) + (x - 2)(x - 4)(x + 3) ≤ 0
(x - 2)(x² - 4x + 3x -12 + 6) ≤ 0
(x - 2)(x² - x -6 ) ≤ 0
D = 1 + 24 = 25
x12=(1+-5)/2 = 3 -2
(x - 2)(x - 3)(x + 2) ≤ 0
применяем метод интервалов
[-2] [2] [3]
x ∈(-∞ -2] U [2 3] пересекаем с ОДЗ x∈(-3 2)
ответ x∈(-3 -2]