Пусть х - первое число, тогда
(х + 4) - второе число,
(х + 4) + 6 = (х + 10) - третье число.
х : (х + 4) = (х + 4) : (х + 10) - отношение чисел
Уравнение:
х/(х+4) = (х+4)/(х+10) - это пропорция
х · (х + 10) = (х + 4) · (х + 4) - свойство пропорции
х² + 10х = (х + 4)²
х² + 10х = х² + 2 · х · 4 + 4²
х² + 10х = х² + 8х + 16
х² + 10х - х² - 8х = 16
2х = 16
х = 16 : 2
х = 8 - первое число
(х + 4) = 8 + 4 = 12 - второе число
(х + 10) = 8 + 10 = 18 - третье число
ответ: числа 8, 12 и 18.
Проверка:
8 : 12 = 12 : 18
0,(6) = 0,(6)
Чтобы найти НОД чисел нужно разложить их на простые множители и перемножить между собой общие множители (подчёркнуты).
Чтобы сократить дробь, нужно числитель и знаменатель разделить на НОД.
1) 24 = 2 * 2 * 2 * 3
60 = 2 * 2 * 3 * 5
НОД (24; 60) = 2 * 2 * 3 = 12

2) 45 = 3 * 3 * 5
105 = 3 * 5 * 7
НОД (45; 105) = 3 * 5 = 15
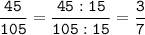
3) 39 = 3 * 13
130 = 2 * 5 * 13
НОД (39; 130) = 13
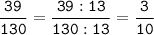
4) 64 = 2 * 2 * 2 * 2 * 2 * 2
144 = 2 * 2 * 2 * 2 * 3 * 3
НОД (64; 144) = 2 * 2 * 2 * 2 = 16
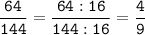
===========================================================
Чтобы найти НОК чисел, нужно разложить их на простые множители и к множителям бОльшего числа добавить недостающие множители (подчёркнуты) и перемножить их между собой.
Наименьшее общее кратное и будет наименьшим общим знаменателем.
1) 12 = 2 * 2 * 3
8 = 2 * 2 * 2
НОК (12; 8) = 2 * 2 * 3 * 2 = 24


2) 9 = 3 * 3
15 = 3 * 5
НОК (9; 15) = 3 * 5 * 3 = 45

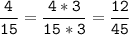
3) 25 = 5 * 5
15 = 3 * 5
НОК (25; 15) = 5 * 5 * 3 = 75
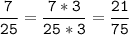
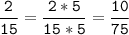
4) 16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
НОК (16; 24) = 2 * 2 * 2 * 3 * 2 = 48
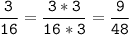
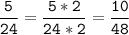
както так)))