Question

Найти область сходимости функционального ряда.

Answer 1

х∈(-∞;  +∞)

Пошаговое объяснение:

Используем признак Вейерштрасса

Для  ряда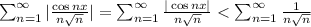 $\sum_{n=1}^\infty|\frac{\cos nx}{n\sqrt{n}} |=\sum_{n=1}^\infty\frac{|\cos nx|}{n\sqrt{n}}<\sum_{n=1}^\infty\frac{1}{n\sqrt{n}}$

существует мажорантный ряд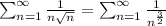 $\sum_{n=1}^\infty\frac{1}{n\sqrt{n}}=\sum_{n=1}^\infty\frac{1}{n^{\frac{3}{2}}}$

Известно, что последний ряд сходится, так как степень в знаменателе больше единицы. Значит существует мажорантный сходящийся ряд по отношению к исходному знакопеременному ряду. По признаку Вейерштрасса исходный ряд сходится. Здесь |cos nx|≤1 независимо от х в поле действительных чисел. Значит х∈R.

Answer 2

Этот ряд при любом х меньше чем ряд 1/(n^1.5), который сходится, потому что 1.5>1

Так что область сходимости - все вещественные числа