Пошаговое объяснение:
1. область определения.
функция определена везде, где знаменатель не равен нюлю
x²-1 ≠ 0 ⇒ х ≠ ±1
ООФ x ∈ R: x≠1 ∪ x≠ -1
2) уравнение касательной
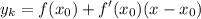
f'(x) = -3x²-6x
f(-5) = 52
f'(-5)= -45
уравнение касательной
y=52+(-45)(x--5)
или
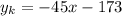
3) экстремумы и монотонность
критические точки ищем при первой производной
f'(x) = 3x²-18x+15
3x²-18x+15 = 0 ⇒ x₁ = 1; x₂ = 5 -это точки экстремума
f(1) = 7 это максимум
f(5) = -25 - это минимум
теперь рассмотрим интервалы монотонности
(-∞ ;1) f'(0) = +15 > 0 - функция возрастает
(1; 5) f'(2) = 3*2² -18*2 +15 = -9 < 0 функция убывает
(5; +∞) f'(10) = 3*10² -18*10 +15 > 0 - функция возрастает
4) экстремумы на промежутке
ищем критические точки
f'(x) = 4 - 2x
4 - 2x = 0 ⇒ x₁ = 2
поскольку нам задана парабола ветвями вниз, то это будет точка максимума и она ∈ [0;4]
f(2) = 6 - это максимум
поскольку нам заданы минимум и максимум на отрезке, ищем значения функции на концах отрезка
f(0) = 2
f(4) = 2
итого имеем
наибольшее значение функции в точке х=2 равно f(2) = 6
наименьшие значения функции на концах отрезка и равны
f(0) = 2 f(4) = 2
︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋ ︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋︋