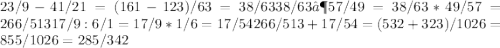
ответ: а) 1 целая 3/8 б) -1/2
Пошаговое объяснение:
а) 1. Найдём разность дробей с равными знаменателями:
5/8 - 16/8 = 5-16 / 8 = - 11/8
2. Так как числитель больше знаменателя, то преобразуем неправильную дробь в смешанное число:
11/8 = 1*8+3 / 8 = 1*8 / 8 + 3/8 = 1 + 3/8
б) 1. Раскроем скобки возле второй дроби:
2 21/26 + (-3 4/13) = 2 21/26 - 3 4/13
2. Преобразуем смешанные числа в неправильные дроби:
первое:
2 21/26 = 21+2*26 / 26 = 73/26
второе:
3 4/13 = 4+3*13 / 13 = 43/13
3. Приведем дроби к наименьшему общему знаменателю:
Найдем наименьшее общее кратное знаменателей дробей 73/26 и 43/13
НОК(26,13) = 26
26/26 = 1 — дополнительный множитель первой дроби
26/13 = 2 — дополнительный множитель второй дроби
73/26 = 73*1 / 26*1 = 73/26
43/13 = 43*2 / 13 * 2 = 43/26
4. Найдем разность дробей с равными знаменателями:
73/26 - 86/26 = 73-86 / 26 = -13/26
5. Упростим дробь:
-13/26 = - 1*3 /2*13 = - 1/2
ответ: 14 детей.
Пошаговое объяснение:
Число детей , у кого на ногах поровну носков, в 4 раза меньше, чем тех, у кого не поровну, значит : было 1/5 детей, у кого на ногах поровну носков и 4/5 детей, у кого не поровну. Когда каждый ребенок снял носок с одной ноги и надел на другую, то детей, у кого носков поровну стало в 2 раза меньше, чем тех, у кого не поровну, значит: стало 1/3 детей, у кого на ногах поровну носков и 2/3 детей, у кого не поровну.
Найдем НОК знаменателей:
НОК(3;5)=15 ; Т.к всего детей меньше 35, и вычисления должны быть в натуральных числах , то наибольшее число детей будет:
15*2=30 (детей) это наибольшее количество детей, которые пошли на прогулку.
30*(1/5)=6 (детей) у кого на ногах было вначале носков поровну. (После переодевания количество носков стало отличаться на 2.)
30*(1/3)=10 (детей) у кого на ногах стало после переодевания носков поровну. (В начале количество носков отличалось на 2.)
30-(6+10)=14 (детей) это наибольшее количество детей в начале прогулки, число носков на ногах которых могло отличаться на 1.