 ⇒
⇒![\int\limits {arccos^22x/ \sqrt{1-4x^2} } \, dx =1/2 \int\limits{t^2} \, dt =t^3/6=[tex]-1/6arccos^32x + C](/tpl/images/0295/9857/58697.png)
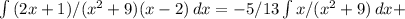
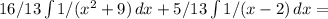
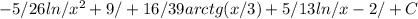
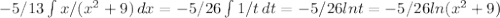
![16/13 \int\limits {1/(x^2+9)} \, dx =16/117 \int\limits {1/[(x/3)^2+1]} \, dx =16/39arctg(x/3)](/tpl/images/0295/9857/6e655.png)
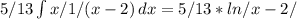
2) 156-33=123 (см)
3) 123:3=41 (см) - длина второй части ленты.
4) 41+18=59 (см) - длина первой части ленты.
5) 41+15=56 (см) - длина третьей части ленты Предположим, что х см длина второй части, тогда (х+18) см длина первой части, а (х+15) см длина третьей части, также из условия задачи известно, что изначальная длина ленты 156 см
согласно этим данным составим и решим уравнение:
х+18+х+х+15=156
3х+33=156
3х=156-33
3х=123
х=123:3
х=41 (см) - длина второй части ленты.
х+18=41+18=59 (см) - длина первой части ленты.
х+15=41+15=56 (см) - длина третьей части ленты.
ответ: 59 см длина первой части ленты; 41 см длина второй части ленты; 56 см длина третьей части ленты.
Проверка:
59+41+56=156 (см) - первоначальная длина ленты.
проверил численным интегрированием